Continuum Mechanics 2 – Material Derivative Numerical Examples
Last month’s post began a detailed study of continuum mechanics by looking at the general structure of the formalism and the specific linkage between the Lagrangian point-of-view, which co-moves along with a material element, and the Eulerian point-of-view, which focuses on specific locations and times as material elements move into and out of these locations.
The material derivative,
\[ \frac{d}{dt} f = \frac{\partial f}{\partial t} + \vec v \cdot \vec \nabla f \; , \]
provides the connection between these points-of-view, relating the time rate-of-change of the field $$f(t,\vec r)$$ as seen by the material element to the derivatives of the field at the instant that element passes through the position $$\vec r$$.
While the derivation of the material derivative given in the last post is mathematically correct, its abstract nature is difficult to internalize. This post presents the material derivative in a variety of contexts to drive home the equivalence between the two points-of-view.
The physical model employed, consists of a material element, a small bit of fluid or elastic material (with enough internal cohesion that is stays as a discernable element), in motion around the Earth, which is, in turn, heated by the Sun. The temperature that the element sees varies as it moves relative to the Earth-Sun line and with time as the Earth moves along its own orbit around the Sun, getting closer or further as the seasons change.
For simplicity, the geometry will be assumed 2-dimensional and will be, predominantly, described in plane polar coordinates $$r$$ and $$\theta$$.
The trajectory will be written as a product a radius function $$R(t) = R_0 + at$$ and a simple linear function for the polar angle $$\Theta = \omega t$$ associated with uniform circular motion ($$a$$ and $$\omega$$ are constants. Depending on the context, the resulting trajectory may be expressed in either cartesian form as
\[ \vec R(t) = (R_0 + at) \left[ \cos(\omega t) \hat e_x + \sin (\omega t) \hat e_y \right] \;\]
and
\[ \vec V(t) = (R_0 + at) \left[ -\sin(\omega t) \hat e_x + \cos(\omega t) \hat e_y \right] \\ + at \left[ \cos(\omega t) \hat e_x + \sin(\omega t) \right] \hat e_y \; , \]
for the position and velocity, respectively, or
\[ \vec R(t) = (R_0 + at) \hat e_r(t) \; \]
and
\[ \vec V(t) = (R_0 + at) \hat e_{\theta}(t) + at \hat e_r(t) \; , \]
for the same in polar form.
Similarly, the temperature field will be written in separable form as a product of 3 functions, $$T_r$$, $$T_{\theta}$$, and $$T_t$$, which are functions solely of $$r$$, $$\theta$$, and $$t$$, respectively. This last assumption, done for convenience, represents no loss of generality. The specific form of each of these will be tailored to each of the three scenarios presented below.
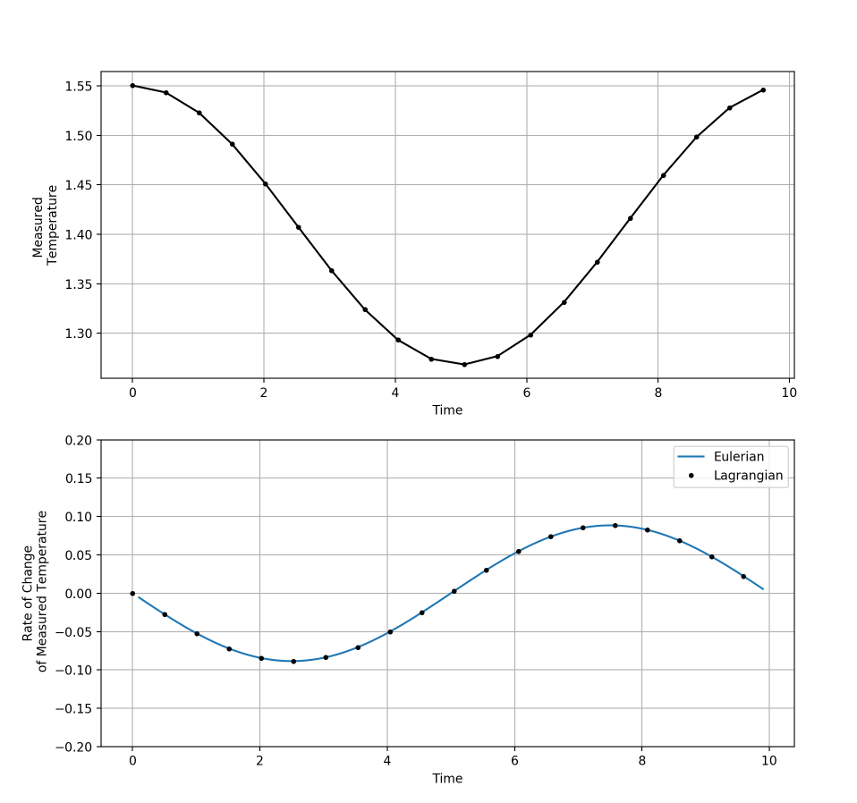
In each scenario, the rate-of-change seen by the element (Lagrangian point-of-view) is calculated by the following process. The position and velocity of the element is evaluated at tabulated times to produce an ephemeris, the temperature is measured at each of the ephemeris points, and then the time rate-of-change of the measured temperature is constructed by using the central difference approximation to the derivative given by
\[ \frac{d}{dt} T = \frac{T(t+\Delta t) – T(t-\Delta t)}{2 t} \; .\]
These values for the time rate-of-change define ‘truth’ in the Lagrangian point-of-view and will be the values against which we will judge the material derivative computation in the Eulerian point-of-view.
Scenario 1 – Time-independent Temperature Field Encountered in a Circular Orbit
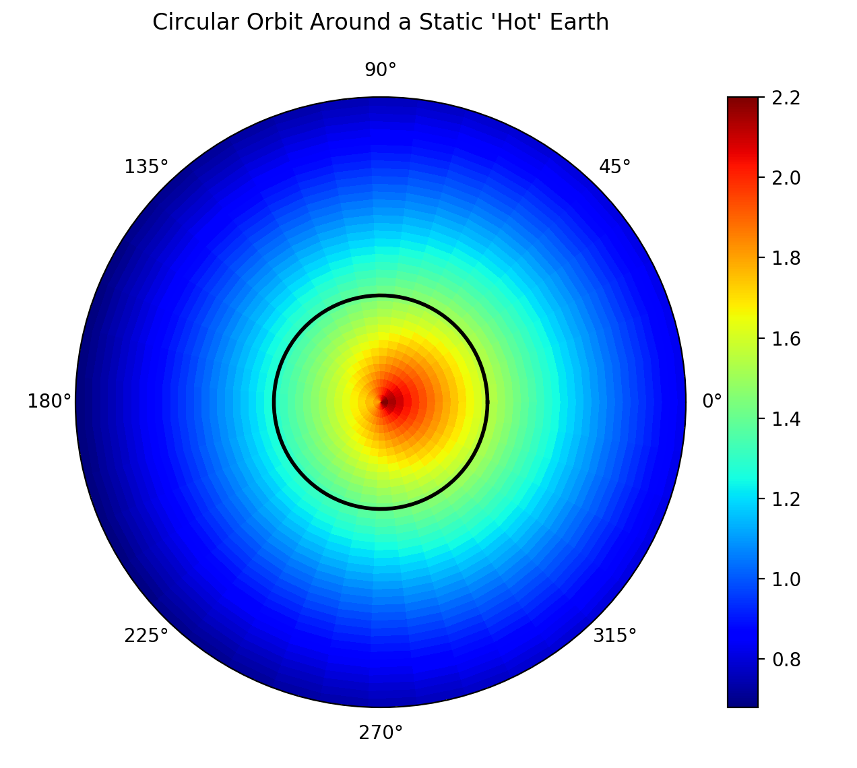
In this scenario, the material element moves in a circular orbit ($$a=0$$) through the temperature field, defined by
\[ T(t,r,\theta) = T_0 (1 + \Delta T \cos(\theta) ) \exp\left(-r/r_0\right) \equiv T_{\theta} T_r \; .\]
This field is an elementary model of a hot Earth radiating its heat into space with a colder side (centered on $$\theta = \pi$$) pointing away from the Sun.
The element’s motion through the field (the colorbar maps the color to the temperature)
leads us to expect a periodic variation in time of the measured temperature, even though the underlying field is static (i.e. time-independent).
The gradient of the field, presented in the best way for numerical programming, is given by:
\[ \vec \nabla T = T_{\theta} T_{r,r} \hat e_r + \frac{1}{r} T_{\theta,\theta} T_r \hat e_{\theta} \; , \]
where:
\[ T_{r,r} \equiv \frac{\partial T_r}{\partial r} = -\frac{1}{r_0} \exp\left(-r/r_0\right) \; \]
and
\[ T_{\theta,\theta} \equiv \frac{\partial T_{\theta}}{\partial \theta} = -T_0 \Delta T \sin(\theta) \; .\]
The velocity in this scenario is entirely in the polar angle direction and is given by
\[ \vec V = R_0 \omega \hat e_{\theta} \; .\]
Since there is no explicit time dependence in the field, the right-hand or Eulerian side of the material derivative is
\[ \vec V \cdot \vec \nabla T = – R_0 \omega \frac{1}{R(t)} T_0 \Delta T \sin(\omega t) \exp\left( -R(t)/r0 \right) \; \, \]
where, it should be emphasized, the field gradients are evaluated at the instantaneous position of the material element.
Comparison of this expression to the Lagrangian truth from the central differences shows excellent agreement.
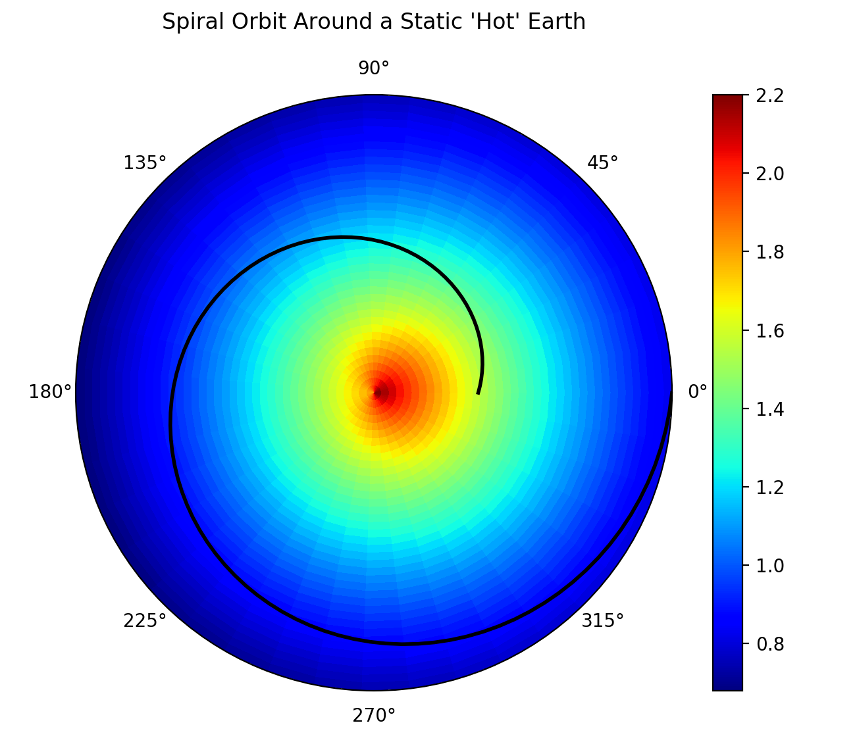
Scenario 2 – Time-independent Temperature Field Encountered in an Out-spiral Trajectory
In this scenario, the underlying temperature field remains the same but the trajectory is an outgoing spiral ($$a>0$$)
and thus there are both radial and polar components of the velocity given by
\[ V_r = a t \]
and
\[ V_{\theta} = (R_0 + a t) \omega \; ,\]
respectively.
The Eulerian side of the material derivative now becomes
\[ \vec V \cdot \vec \nabla T = – a t \frac{1}{r_0} \exp\left(-r/r_0\right) T_0 (1 + \Delta T \cos(\omega t)) \\ – (R_0 + at) \omega \frac{1}{R(t)} T_0 \Delta T \sin(\omega t) \exp\left( -R(t)/r0 \right) \; . \]
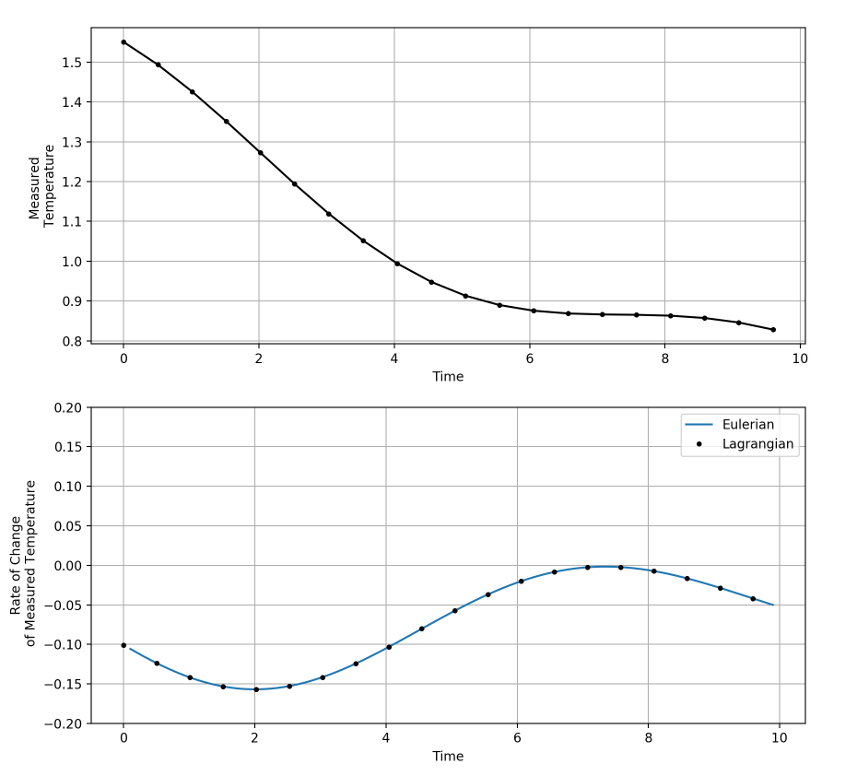
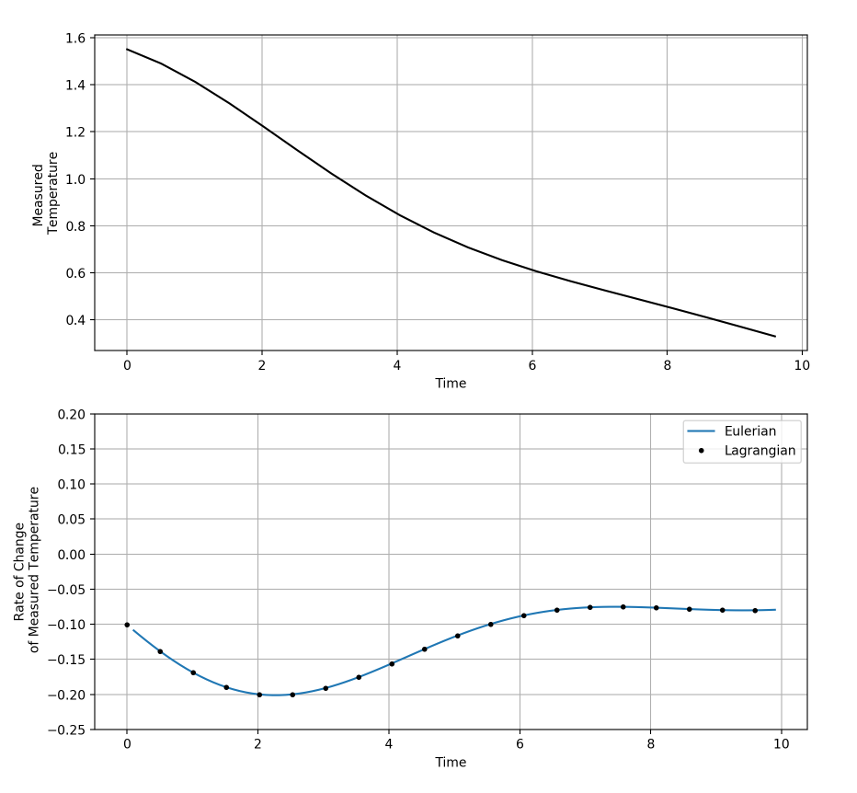
The measured temperature computed along the trajectory shows an overall, but not monotonic, decrease in the value, with the small bump upwards occurring when the material element swings to the hot side. The time rate-of-change calculated in both ways again shows excellent agreement.
Scenario 3 – Time-dependent Temperature Field Encountered in an Out-spiral Trajectory
In this final scenario every possible variation is covered. The trajectory is the same out-spiral used in Scenario 2. To the spatial variation of the temperature field is added a simple time-dependence so that the temperature field is now:
\[ T(t,r,\theta) = T_r T_{\theta} exp(-t^2/\tau^2) \; .\]
The material derivative now includes a time variation of the field and the Eulerian form is
\[ \frac{\partial T}{\partial t} + \vec V \cdot \vec \nabla T = -\frac{2t}{\tau^2} T_t T_r T_{\theta} – a t \frac{1}{r_0} T_t T_r T_{\theta} \\ – (R_0 + at) \omega \frac{1}{R(t)} T_0 \Delta T \sin(\omega t) T_t T_r \; , \]
where $$T_r$$ and $$T_{\theta}$$ are evaluated at the ephemeris point of the material element $$\vec R(t)$$.
Once again, the agreement is excellent, demonstrating in a concrete fashion, the equivalence of Lagrangian and Eulerian points-of-view.