Continuum Mechanics 5 – The Stress Tensor
The last set of posts have centered on describing the kinematics of continua by defining the material derivative and the Reynolds and Flux transport theorems. But kinematics by themselves are not much fun without being able to describe the forces that cause the kinematics. Forces within the realm of continuum mechanics are generally called stresses and the changes that they cause in the position and velocity of an element are called strains and strain rates.
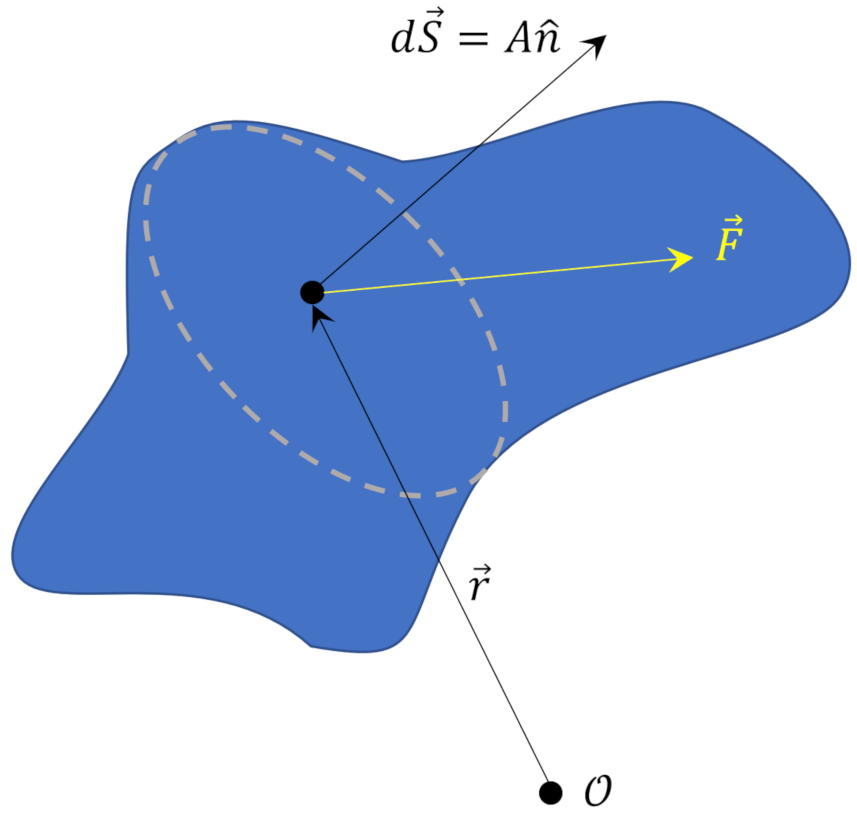
The central player in determining a continuum’s dynamics is the stress tensor, which is a rank two tensor that takes in the position vector and the area times the normal to a surface in the continuum as inputs and returns the vector of force acting on that surface at that point. Pictorially, the situation looks like
while in abstract mathematical notation the tensor is described as
\[ \mathbf{T}(\vec r) \cdot d\vec S = \vec F \; , \]
where $$A$$ is the differential area of the face of the continuum (all of these results are exact in the limit as the size of the fluid element goes to zero).
There are two points worth discussing. First, it may not be at all obvious why the force should have components that do not lie along the surface normal. Second, assuming a satisfactory answer to the first question, why is the relationship between the force and the surface normal linear, as required for it to be a tensor relation.
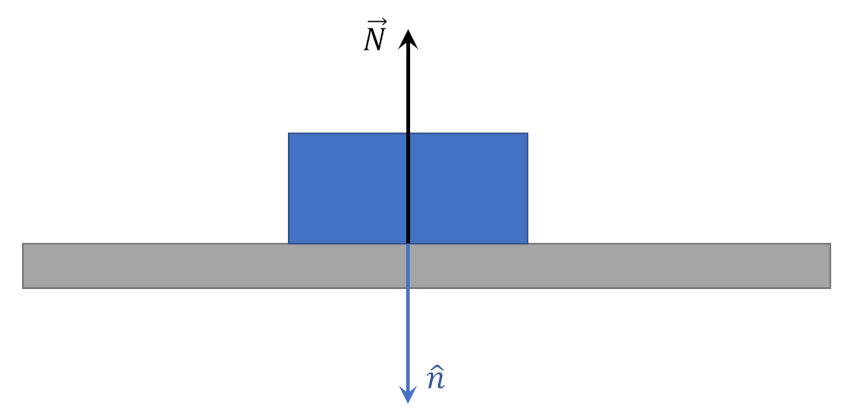
The first question is the easier of the two to answer. Consider the surface force a block experiences as it rests upon a table top.
In this case, the normal force $$\vec N$$ lies anti-parallel to the unit normal $$\hat n$$ (note that the sign is matter of convention and different authors define a positive normal force to be when the force acts to compress the element, other authors when the force seeks to extend the element). Gravity plays no role here since it acts on each part of the body in the same way resulting in no stress (this fails to hold in a non-uniform field). The same situation would hold for a block sliding down a frictionless plane as the only stress on the surface of the block touching the incline plane is still normal to the surface.
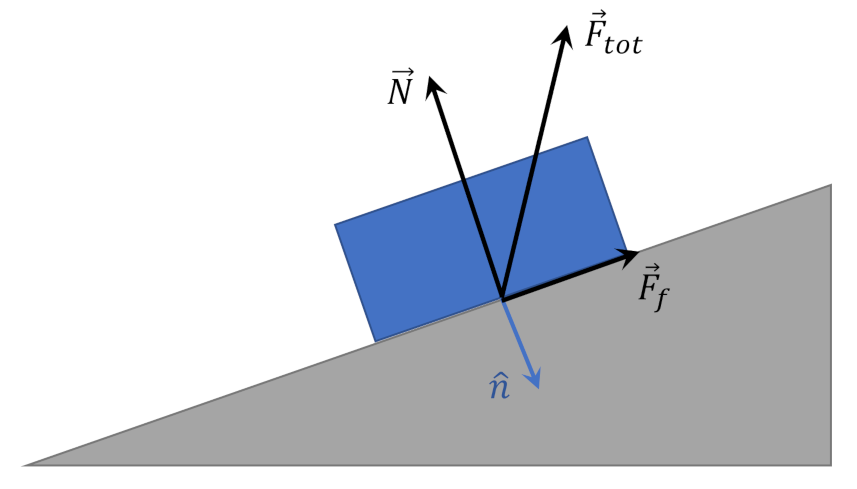
However, the addition of friction ($${\vec F}_{f}$$) between the block and the plane creates a situation where the total force, $${\vec F}_{tot}$$, acting on the surface no longer lies along (either parallel or anti-parallel) to the surface normal. The component of force parallel to the interface between the block and the plane is a known as a shear force, with friction being the cause in this case.
If the angle of the incline plane is varied, the surface normal changes direction and the total force responds in kind, thus establishing the dependence on $$\hat n$$. If the roughness of the plane varies along its length, the direction and magnitude of $${\vec F}_{tot}$$ will also vary, thus establishing the dependence of the position vector $$\vec r$$. Properly interpreted, the concept of a force acting on a surface of a continuum that falls in a direction different from the surfaces unit normal and that has a spatial dependence can be found even in one of the most familiar scenarios from basic mechanics.
The response of a continuum to the application of a shear force is one of the primary ways in which matter is separated into its various phases (solid, liquid, gas, or plasma) and will the subject of future posts.
In order to answer why the mapping from surface normal to force should be linear, one must demonstrate the mapping is linear with respect to both scalar multiplication and vector addition as summarized in
\[ {\mathbf T} \cdot (c_1 d {\vec S}_1 + c_2 d {\vec S}_2 ) = c_1 {\mathbf T} \cdot d {\vec S}_1 + d {\mathbf T} \cdot d {\vec S_2} \; . \]
Symon covers this point nicely in Section 10.6 of his Mechanics (2nd edition) and I won’t bother to repeat the steps in detail. The key observation is that in shrinking the fluid element to zero, for example by multiplying by a small factor that Symon calls $$\alpha$$, the inertial side of Newton’s second law scales as $$\alpha^3$$, since it is proportional to density times volume, while the dynamic side of Newton’s second law scales as $$\alpha^2$$, since the force is proportional to the area. Symon then considers this scaling applied to a triangular prism where the normal to one face can be expressed in terms of the other two as $$d {\vec S}_3 = – d {\vec S}_1 – d {\vec S}_2$$. The only way to prevent a catastrophic build up in acceleration on the fluid element is if the sum the forces over all the faces is identically zero which can only happen if the mapping is linear (i.e. a tensor relationship).
There is one further point worth noting. The stress tensor $${\mathbf T}$$ must be a symmetric tensor; in index notation $$T_{ij} = T_{ji}$$. Thorne and Blandford show in Chapter 1 of Modern Classical Physics that the symmetry of the stress tensor follows by considering the effects of the torques (shear forces) on four sides of a cubical element with side length $$L$$. In their example, they determine the torque on the faces whose normals are parallel to the $$x$$-axis due to shears in the $$y$$-direction (i.e. $$T_{xy}$$) and find that the total torque is
\[ {\vec \tau}_z = T_{xy} L^3/2 \; .\]
Likewise, the torque on the faces whose normals are parallel to the $$y$$-axis due to shears in the $$x$$-direction has a total torque of
\[ {\vec \tau}_z = T_{yx} L^3/2 \; .\]
The sum of these torques has to equal to the time rate-of-change of the angular momentum, which gives
\[ (T_{xy} – T_{yx} ) L^3 = \frac{1}{6} \rho L^5 \frac{d L_z}{d t} \; .\]
Using a scaling argument similar to Symon’s one discussed above, one concludes that as $$L$$ goes to zero, the only physical way to prevent infinitely large angular accelerations is to have
\[ T_{xy} = T_{yx} \; .\]
This generalizes immediately to stress tensor as a whole being symmetric.
This analysis then completes the basic characterization of the stresses in a continuum. The next post will look at how materials respond to the application of the stresses.