Of Milk and Entropy
Last month’s column teased the idea that there was a challenge to the common wisdom that states that the reason that the traditional (T) expression for the entropy of a classical (C) gas of distinguishable (D) particles, given by
\[ S_{TCD} = k N \left[ \ln V + \frac{3}{2} \ln \frac{E}{N} + X \right] \; , \]
where $X$ is some constant, fails to be extensive is that classical mechanics overcounts the number of possible configurations. A division of the partition function by $N!$ yields an extensive expression
\[ S_{T} = k N \left[ \ln \frac{V}{N} + \frac{3}{2} \ln \frac{E}{N} + X \right] \; , \]
as the ‘correct one’ and the conclusion is a philosophical one: there is no escaping quantum statistics; all gases are made up of indistinguishable (I) particles.
This conclusion seems ably rebutted by a paper entitled Statistical mechanics of colloids and Boltzmann’s definition of the entropy, by Robert H. Swendsen in 2006 in the American Journal of Physics. Swendsen’s argument centers on looking at whole milk – the kind you can buy in any supermarket or convenience store.
While I must confess that even though I purchase whole milk regularly and was well aware that the term ‘homogenized’ attached to it, I never really bothered to understand just what was made homogeneous. The basic notion is that the homogenized milk is a colloid with tiny fat and protein globules (Swendsen states characteristic sizes of the fat globules of ~0.5 microns) separated in a water medium. Whole milk, which is 4
There are two key assumptions that Swendsen makes at the core of his analysis of whole milk as a classical colloid:
- The globules are distinguishable
- The globules constitute a gas
That the globules are distinguishable is strongly supported by the fact that at a diameter of ~0.5 microns, there are approximately $10^{9}$ atoms (give or take an order of magnitude) contained within each globule, and, so, it would be extremely unlikely that any two globules would contain exactly the same number of atoms. The odds of finding identical globules drops many orders of magnitude more once one considers that each globule will contain some amount of foreign contaminants so that both the composition and the number of atoms found within any given globule will likely be unique and thus each globule will be microscopically distinguishable.
That the globules can be model as an ideal gas takes a bit more thought. The key features of an ideal gas are that it is a collection of similar objects that only interact with each other over a very short range and that the time between interactions is large compared to the duration of the interaction. Despite the fact that the globules are suspended in water, a substance which continuously jostles the individual globules, doesn’t alter the fact that they interact with other fat globules through a short-range electrostatic repulsion only occasionally (on the order of 4
With Swendsen’s two assumptions well-supported, we are now equipped to argue against the conclusion that quantum mechanics is inescapable. Here we have a gas of distinguishable particles, all much larger than an atom so that quantum statistics can hold no sway, for which the traditional expression for entropy predicts startlingly wrong conclusions. One, we’ve already encountered in the Gibbs paradox discussion in the last post. The other, which is a variation, also deals with mixing and goes something like this.
Imagine that we divide a tank of total volume into two subdivisions $V = V_1 + V_2$ subject to the constraint $V_1 > V_2$. The larger sub-volume $V_1$ is filled with whole milk and the smaller sub-volume $V_2$ is filled with skim milk (completely devoid of fat globules). Let $N$ be the total number of fat globules in the system, which are initially contained in $V_1$ and $E = E_1$ be their total energy. For simplicity, we can also assume that the average energy per particle $\epsilon$ remains fixed (no heat transfer and no work done). The initial entropy of the system given by the traditional formula is
\[ S_{TCD,initial} = k N \left[ \ln V_1 + \frac{3}{2} \ln \epsilon + X \right] \; . \]
We then imagine opening a small port for the two systems to mix and then closing it. The final entropy is
\[ S_{TCD,final} = k N_1 \left[ \ln V_1 + \frac{3}{2} \ln \epsilon + X \right] + k N_2 \left[ \ln V_2 + \frac{3}{2} \ln \epsilon + X \right] \; . \]
The difference in the entropy is then
\[ \Delta S_{TCD} = k N_1 \ln V_1 + k N_2 \ln V_2 – k N \ln V_1 = k N_2 \left( \ln V_2 – \ln V_1 \right) = k N_2 \ln \left( \frac{V_2}{V_1} \right) \; . \]
And here is the problem: given that by construction $V2 < V1$ the entropy is always negative, even though mixing is an irreversible process; it takes work to restore the system to its ‘before’ state (macroscopically that all the globules are back in the larger volume if not precisely at the same microstate of positions ${\vec r}_i$ and velocities ${\vec v}_i$.
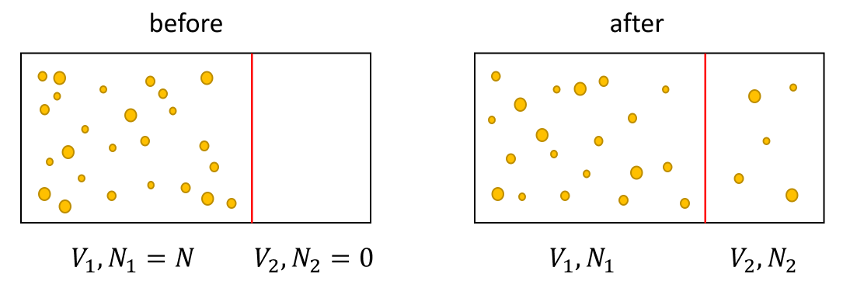
This second inconsistency (and likely there are others) further emphasizes that the classical expression is deeply flawed and, of course, we already knew this. But we can’t resort to quantum mechanics to come in save the day, as was done with simpler gases, since this approach is also deeply flawed as each object in this system is also distinguishable.
Swendsen resolves this problem by arguing that the methodology that led to the classical expression is wrong because it makes entropy related to the volume in phase space and not to the probability. To quote Swendsen:
Oddly enough, Boltzmann would not have encountered these problems, because he would not have used Eq.1 [for $S_{TCD}$]. He wrote the entropy (in modern notation) as
\[ S_{dist} = kN \left[ \ln \frac{V}{N} + \frac{3}{2} \ln \frac{E}{N} + X + 1\right] \; .\] If we use [this equation], the entropy remains constant in the first experiment when the wall between the two subvolumes of milk is either removed or reinserted, as is appropriate for a reversible process. For the second experiment, it is easy to show that $S_{dist,total}$ is always positive; the entropy increases as it must for an irreversible process.Next blog will delve into this question about probability a bit more to show how Monte Carlo simulations dealing with microstates dovetail with entropy and these observations.
