Carnot, Clausius, and Kelvin
This month we were return to our exploration of entropy after our brief detour into field theory. The earlier posts explored the definition of entropy derived from the statistical mechanics. In this installment, we return to the thermodynamic roots of entropy that originated in the analysis of the 19th Century. Our key players in this drama are Sadi Carnot, Lord Kelvin, and Rudolph Clasius, who will be with us both here and for several of the following posts.
This analysis closely follows the presentation found in Enrico Fermi’s book Thermodynamics with some additional extensions in the logic and new, explanatory diagrams that attempt to provide a cleaner approach to traditional material.
Thermodynamics rests upon the idea of a system in equilibrium so that we can characterize it in terms of a very small number of state variables compared with the overwhelmingly enormous number of degrees of freedom the system possesses. A bottle of water is a good poster child for a system in equilibrium. The bottle can be described by the amount of water $m$ (or the number of moles $n$), the volume it occupies $V$, its temperature $T$, pressure $P$, and the like. Even if the water were not pure and we were forced to also specify the percentage of impurities by type there would still be far, far fewer numbers to specify than the incredibly astronomical number of position and velocity components required to describe the state as Newton would. The state variables are completely independent of how the system made it into that configuration. Their values represent average quantities where individual, finer-grained fluctuations are smeared out. There are two state variables that stand above the rest both in importance: the internal energy $U$ and the entropy $S$.
The internal energy is relatively familiar to us based on its analogy to the traditional energies defined in classical mechanics and electrodynamics. That said, it took quite a long time before it was appreciated in the mid-1800s that mechanical energy and heat were equivalent. When the dust had settled, the first law of thermodynamics had been postulated as
\[ \Delta U = Q – W \; , \]
where $Q$ is the heat that enters or leaves the system and $W$ the work done by the system on its surroundings. The sign convention is such that heat entering and work performed are both positive quantities. If one regards energy as the ‘currency’ for physical transactions, then the first law amounts to an accounting principle that says the books must balance and, in this regard, it is relatively easy to understand the physical content.
The entropy, on the other hand, is more difficult to summarize succinctly. Many people can offer euphemisms stating that the principle of entropy means that there is ‘no free lunch’ or that it ‘forbids perpetual motion’ but these euphemisms don’t provide much in the way of physical understanding.
There are several steps in providing a firm understanding of entropy. The rest of this post centers on the first step which involves the different ways of expressing the limitations the second law recognizes in the conversion between work and heat.
We start by looking at the isothermal expansion of an ideal gas, in which a flame provides the heat which causes the expantion. Since the internal energy of an ideal gas only depends on temperature, as long as the temperature remains constant, there is no change in the internal energy $\Delta U = 0$. Then from the first law $W = Q$, which means that all of heat energy is changed into the work needed to raise the piston.
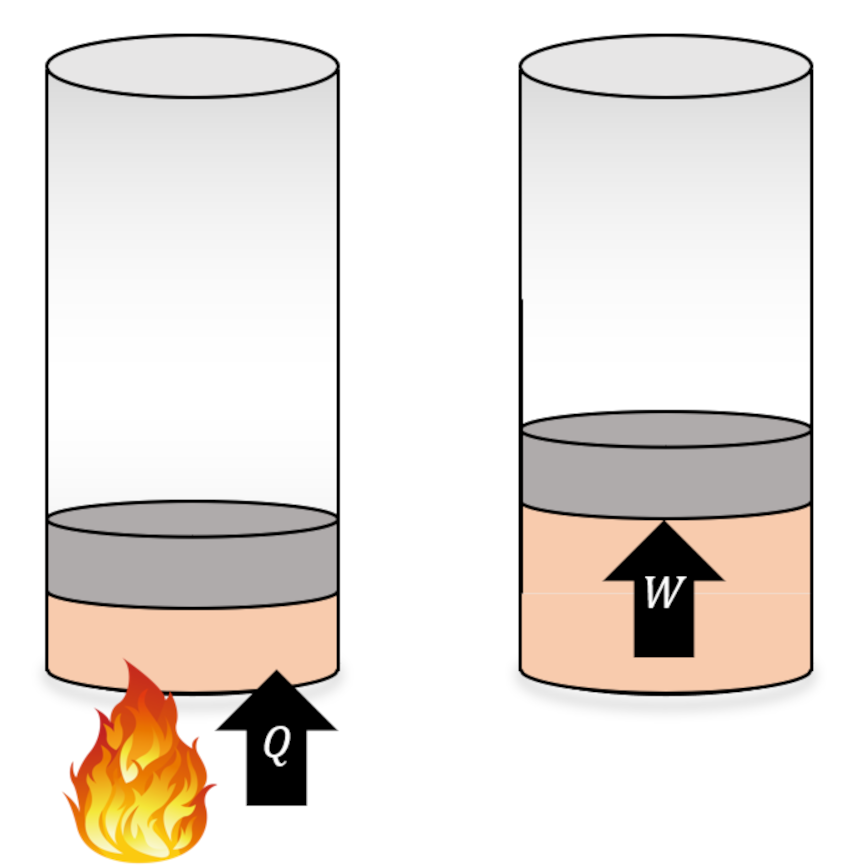
It natural to ask if all physical processes allow for a complete conversion of heat to work as allowed by the first law whenever $\Delta U = 0$ or are there limitations on how efficient arbitrary physical processes can be?
After much analysis and experimentation, most of which was done in the 1800s, the second law of thermodynamics emerged with a clear set of limitations for how changes between heat and work are made. Its modern form expresses the statement in terms of entropy but we will avoid it in favor of more macroscopic statements.
Fermi provides two postulates that capture different aspects of the second law. The first postulate, attributed to Lord Kelvin, states that:
Graphically this forbidden process is represented on a $PVT$ diagram as follows.
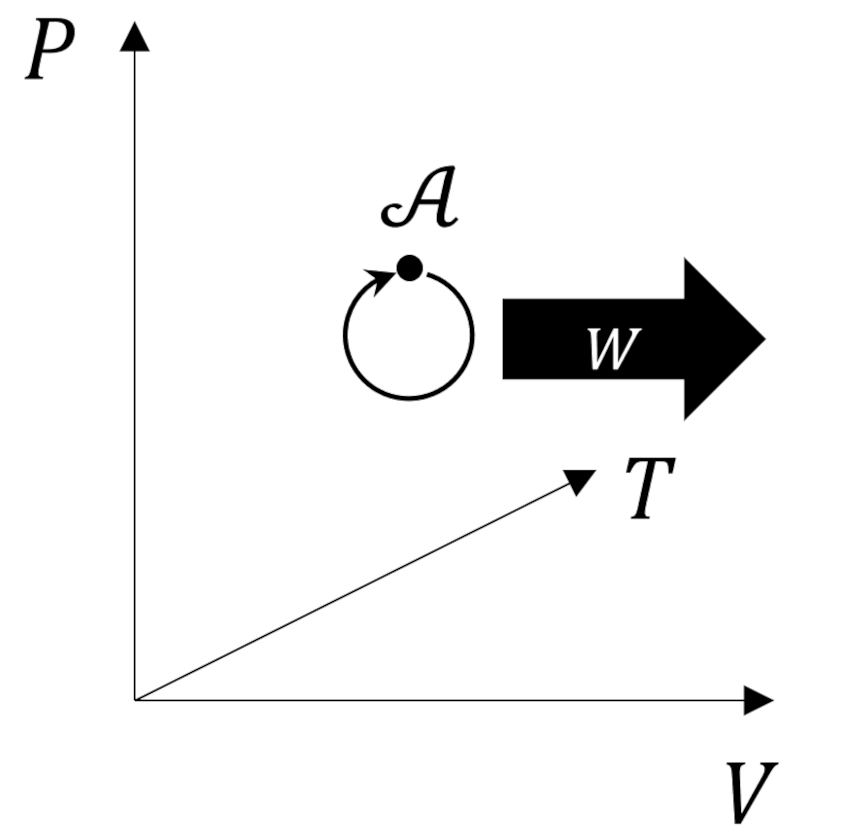
The circular arc reminds us that the state of the system must remain unchanged at the end of the transformation.
The second postulate, attributed to Clausius, states
The graphical representation of this forbidden process as follows.
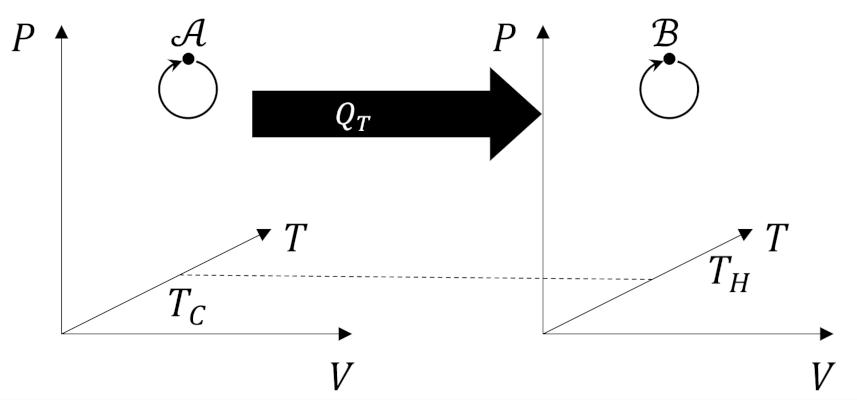
Note that both postulates rule out as impossible certain transformations that leave the state of the system otherwise unchanged (“only final result is…”). Since the state of system is unchanged we will focus on cyclic processes, of the kind used in engines, in which a complete circuit returns the system to its original state ($\Delta U = 0$) with some fraction of the heat absorbed being transformed into work.
The textbook example of a cyclic process is the Carnot cycle, which operates a system between two thermal reservoirs with temperatures $T_C$ and $T_H$ (with $T_C < T_H$).
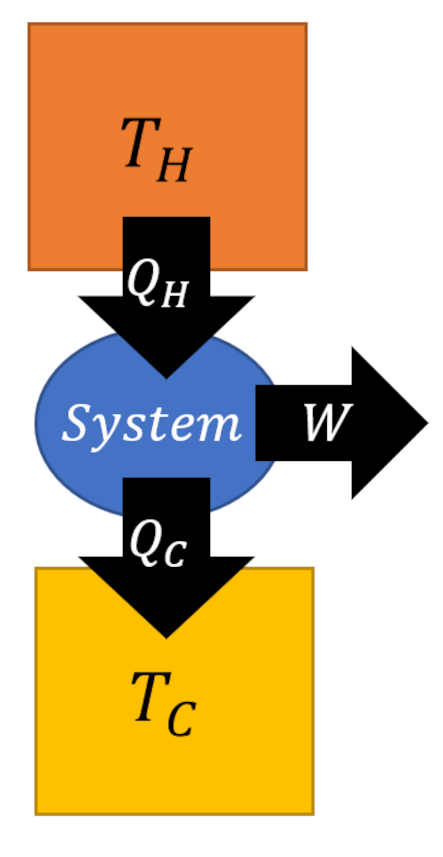
While the details of the Carnot cycle will be explored in the next post, for our purposes the final result relating the work derived to the heat exchanged given by
\[ W = Q_H – Q_C \; \]
will be all that is needed.
Fermi devotes a large amount of effort showing that the Kelvin and Clausius postulates are logically equivalent and are different facets of the same underlying limitations of the second law.
The first part of the proof, that Kelvin’s postulate implies the Clausius postulate, is the easiest to understand. Suppose that the Kelvin postulate were false. Then we could extract from system $A$ some work $W$ leaving system $A$ otherwise unchanged. We then use the work to raise a block up an inclined plane gaining gravitational potential energy. We then let the block slide down the plane using friction to transform the potential energy into heat which we can then dump to the hot reservoir in system $B$, thus violating the Clausius postulate.
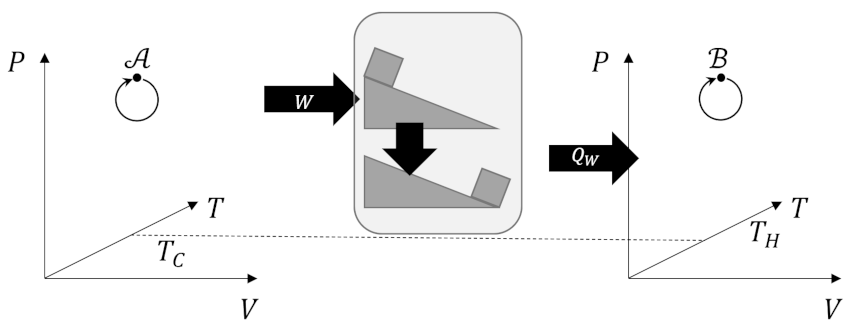
The converse leg of the proof, that the Clausius postulate implies the Kelvin postulate, is a bit more difficult. Suppose that the Clausius postulate were false and that it were possible to transfer some heat $Q_H$ from the cold reservoir at temperature $T_C$ with no other changes in the system to the hot reservoir $Q_H$. As long as the amount of heat is consistent with what is normally adsorbed from by a Carnot cycle to produce an amount of work $W$ we then find that we can return the hot reservoir to its original state with no additional changes. We could then use the Carnot cycle to adsorb this heat to produce some work $W$ thus extracting heat from the hot reservoir without any additional changes in violation of the Kelvin postulate.
The logical equivalence of the Kelvin and Clausius postulates demonstrate that these various limitations are different facets of the second law. This logical structure serves as the launching pad for exploring the concept of entropy from the macroscopic point-of-view.
[Note added after publication – the equivalence between the Kelvin and Clausius postulates is nicely described here.]
