Carnot Cycle
In the last post, we explored Kelvin’s and Clausius’ postulates and found that each of them, in their own way, put limits on the way in which energy could be exchanged in physical systems. We also showed that each of them logically implied the other thereby demonstrating that both were two separate facets of the second law and that a particular result of the Carnot cycle was an integral part of the proof. Now it is time to take a much deeper look at the Carnot cycle and the preeminent place it holds in understanding entropy. Several of the arguments presented here closely mirror those in Carter’s Classical and Statistical Thermodynamics and several of the figures and the argument about the efficiency of the Carnot cycle were inspired by the Fundamentals of Physics by Halliday, Resnick, and Walker.
The Carnot cycle is a special kind of engine or refrigerator depending on how it is run. For clarity, we define engines and refrigerators as machines that execute a set of thermodynamic processes on a physical system, called the working substance, that result in some in the transfer of energy, either in the form or work or heat, but which return the working substance to its initial state. Taken together, the set of processes is called a cycle.
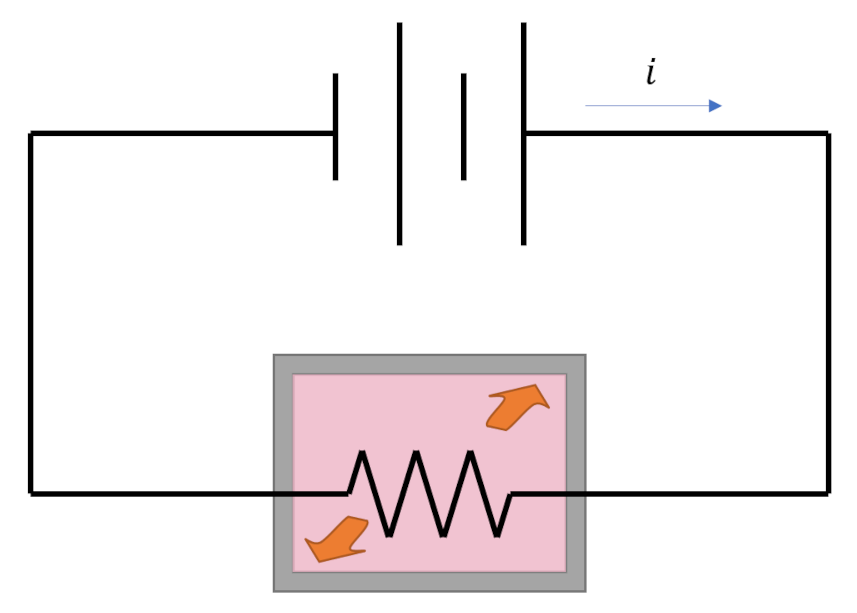
Any thermodynamic process connects an initial state ${\mathcal A}$ to a terminal state ${\mathcal B}$ through a locus of intermediate thermodynamic states. Thermodynamic processes fall into one of two broad categories: reversible and irreversible, with the key difference being that reversible processes naturally run from in the opposite direction (${\mathcal B}$ to ${\mathcal A}$) while irreversible processes do not (hence their names). An example of a reversible process in which energy is exchanged is an elastic collision between two balls. A movie of the collision looks physically reasonable whether it is run forwards or backwards. An example of an irreversible process is the heating of a tank of water by a resistor (of resistance $R$) powered by a battery delivering a current $i$. The heat delivered to the tank during some time span $\Delta t$ is $Q = {\mathcal P} \Delta t = i^2 R \Delta t$. That amount of heat raises the temperature of the tank at the expense of depleting an equal amount of stored energy in the battery. This process looks natural but none of us would expect that we could recharge the battery simply by cooling the tank back to original temperature. This one-way character of irreversible processes gives the physical world the ‘arrow of time’ and many consider it to be one of the hallmarks of entropy.
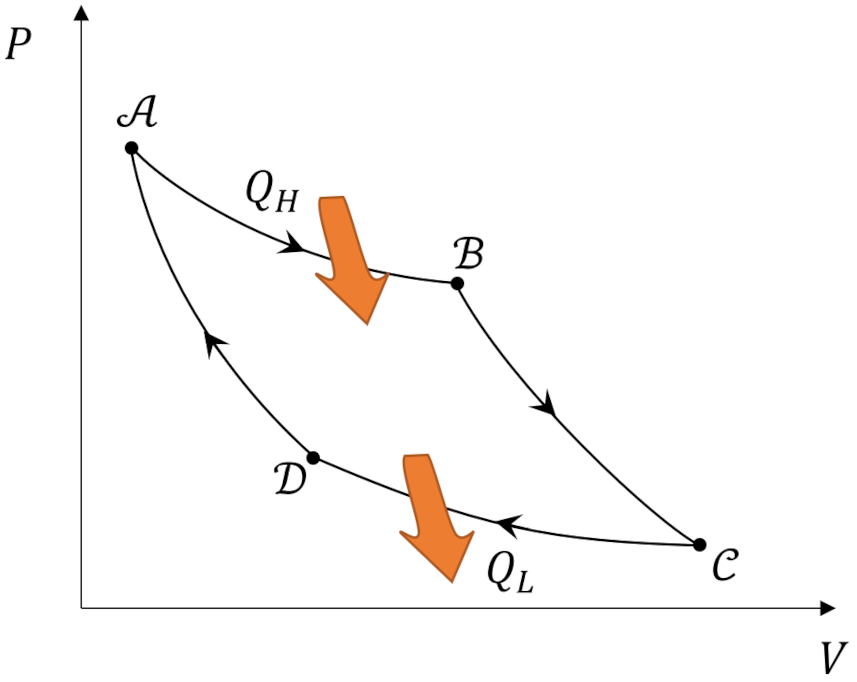
What makes the Carnot cycle so special is that it represents an ideal engine that operates between two heat reservoirs in which all the processes are reversible. It consists of four steps: ${\mathcal A} \rightarrow {\mathcal B} \rightarrow {\mathcal C} \rightarrow {\mathcal D} \rightarrow {\mathcal A}$.
In the first step (${\mathcal A} \rightarrow {\mathcal B}$) the working substance absorbs $Q_H$ from the high temperature reservoir such that it isothermally expands and performs positive work. In the second step (${\mathcal B} \rightarrow {\mathcal C}$) the working substance expands adiabatically ($Q=0$) while it also does positive work. The third step (${\mathcal C} \rightarrow {\mathcal D}$) consists of the working substance being isothermally compressed by dumping $Q_L$ to the cold temperature reservoir will having work done on it (i.e., negative work is done by the system). In the fourth step (${\mathcal D} \rightarrow {\mathcal A}$), the working substance is returned to its initial state by being adiabatically compressed.
Theorists usually represent the Carnot cycle visually as a set of curves plotted in the pressure-volume ($PV$) plane.
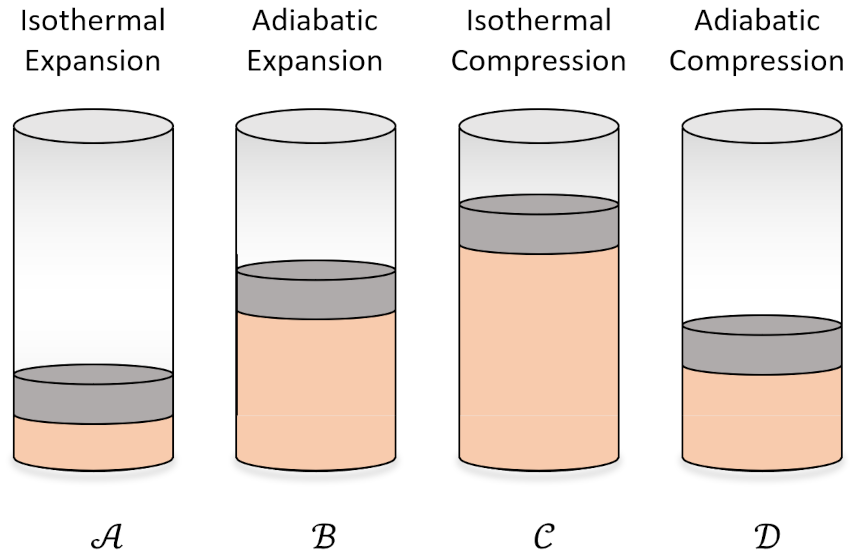
We typically imagine the working substance as an ideal gas. In this case, the abstract steps of the Carnot cycle become familiar processes in terms of the usual cylinder-and-piston arrangement.
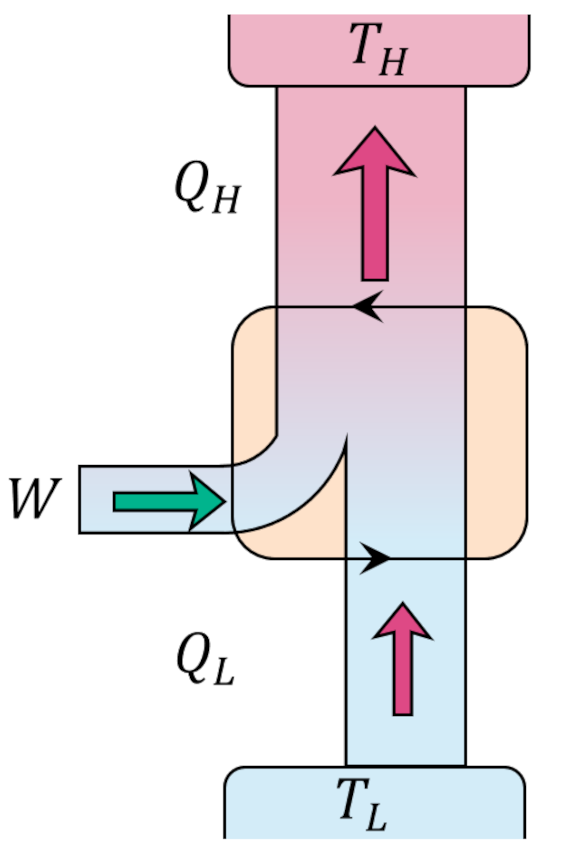
Since the change in internal energy of the system must be zero (the gas ends in the same state that it started in), the first law tells us that the work delivered by the engine $W = |Q_H| – |Q_C|$. Standard practice is to visualize an engine (executing the Carnot cycle or otherwise) abstractly as an systems of interacting boxes that take in and dump heat of quantities $Q_H$ and $Q_L$, respectively, in the process delivering work of amount $W$.
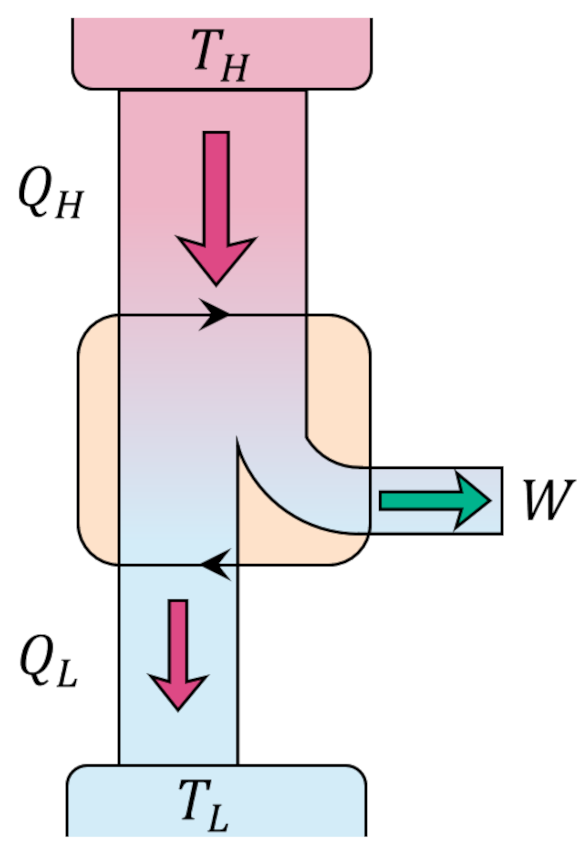
The efficiency of the engine is the fraction of the heat energy that enters the engine that results in useful work and is given by
\[ \epsilon = \frac{W}{|Q_H|} = 1 – \frac{|Q_C|}{|Q_H|} \; . \]
Since every process is reversible, the Carnot cycle can be operated in the opposite order giving a refrigerator that is able to move heat from the lower temperature reservoir to the higher temperature reservoir at the expense of work being provided to the cycle rather than being delivered.
We should now ask if there are any engines that can operate more efficiently than the Carnot cycle. In the process of answering this question in the negative we will see more clearly the connections with Kelvin’s and Clausius’ postulates and will understand why the Carnot cycle has a preeminent position in the field of thermodynamics.
We start our answer by conjecturing that there exists an engine, call it Engine X, whose operating efficiency is better than the Carnot cycle,
\[ \epsilon_X > \epsilon_{Carnot} \; .\]
This assumption doesn’t mean that Engine X takes in the same amount of heat as the Carnot engine nor dumps the same amount but simply that it delivers a given amount of work $W$ as a larger fraction of whatever it takes in. Thus, if the Engine X absorbs $Q’_H$ joules from the higher reservoir to deliver $W$ joules of work then
\[ \frac{|W|}{|Q’_H|} > \frac{|W|}{|Q_H|} \; . \]
This inequality simplifies to
\[ |Q_H| > |Q’_H| \; .\]
By the first law,
\[ |Q_H| – |Q_L| = |W| = |Q’_H| – |Q’_L| \; , \]
which can be rewritten as
\[ |Q_H| – |Q’_H| = |Q_L| – |Q’_L| \; .\]
From our previous analysis of the efficiency, the quantity on the left-hand side is positive and so must be the quantity on the right-hand. By using the work delivered by Engine X to power a Carnot refrigerator
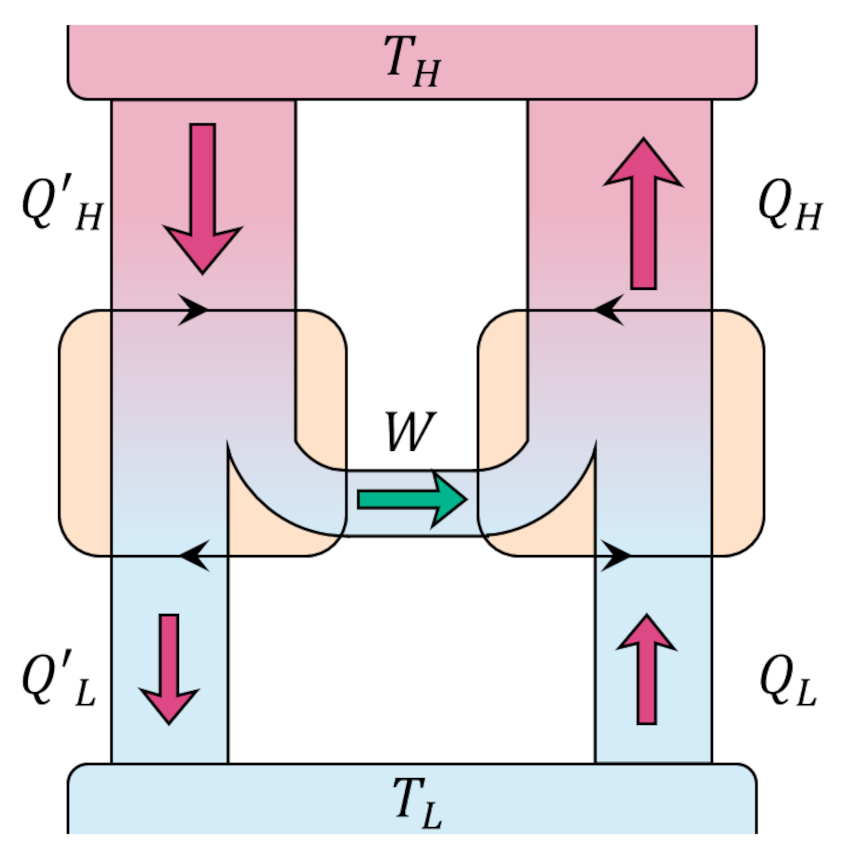
we can create a process whose only effect is to move heat from a colder reservoir to warmer one directly violating the Clausius postulate. If we accept the Clausius postulate we must reject the idea that any engine can be more efficient than the Carnot engine.
Two points in conclusion are worth making. First, we might have expected this outcome given the special nature of reversible processes. Second, given the Carnot cycle’s position as the gold standard of thermodynamics it should come as no surprise that we can always decompose an arbitrary process

into Carnot subprocesses
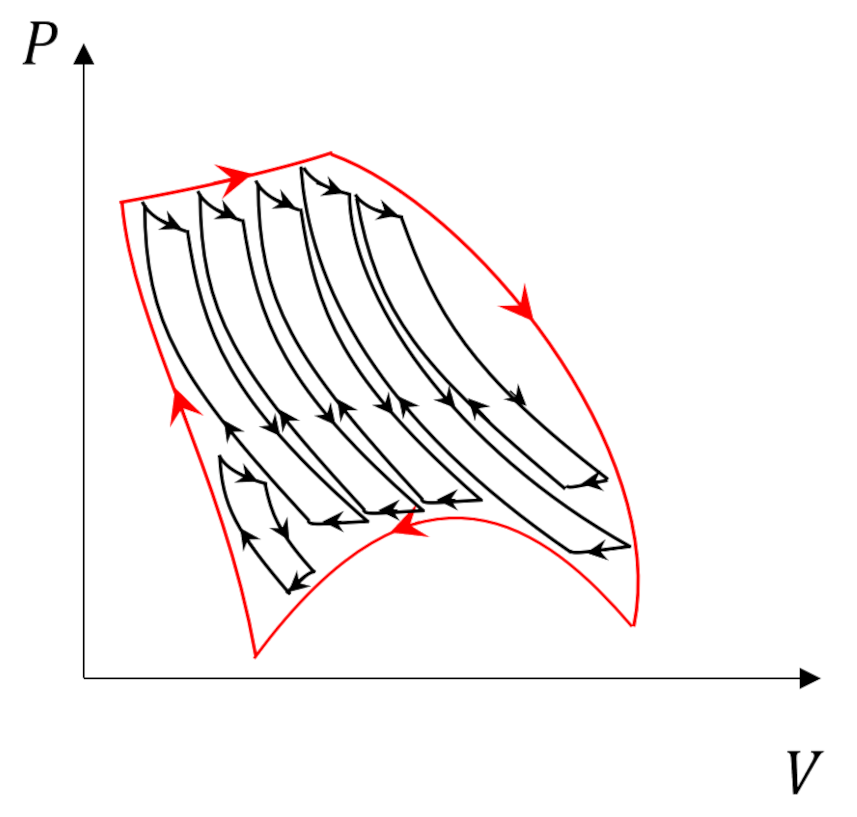
whose internal adiabats cancel and whose efficiency and total energy exchange can be determined by adding the individual subprocesses together (credit to Carter for making this point so clearly).
Next month, we’ll recast the Carnot efficiency in light of using an ideal gas as the working substance and will begin to see the emergence of entropy.
