Entropy and The Second Law
The last post derived the Clausius inequality
\[ \oint \frac{{\tilde d} Q}{T} \leq 0 \; , \]
using a rather subtle and clever technique (presented by Fermi in his book Thermodynamics without further attribution, although it is certain that the argument dates back probably more than fifty years earlier) in which a complex cyclical process was augmented with a set of Carnot cycles that interacted with the original reservoirs and an external heat reservoir called the base. By encapsulating the original cycle and these auxiliary Carnot cycles as a single, black box engine and then invoking Kelvin’s postulate on their total interaction with the base, we were able to arrive at the expression above, with the equality holding only in the limiting case that the original cycle was reversible.
Since an earlier post demonstrated that Kelvin’s and Clausius’s postulates (both of which essentially say that perpetual motion is impossible) were different facets of the second law and Kelvin’s postulate is used to derive the Clausius inequality, it is clear the inequality is yet another expression of the second law. The advantage of this third way of expressing the second law is that, as a mathematical expression, it motivated the definition of entropy, which has dominated the conversation ever after. The quantitative nature of the definition of entropy allows for two useful innovations: 1) the numerical determination for whether a process is allowed or disallowed to proceed spontaneously and 2) and rewriting of the first law in terms of $S$ since it is a state variable. Let’s deal with each in turn.
By definition, spontaneous processes occur naturally in a single direction; heat flows from a warmer body to a colder one; some chemical reactions run only in one direction, eggs that fall on the ground break never to reassemble themselves; and so on. Running movies of these processes backwards looks unnatural even though movies of billiard ball collisions and the motion of celestial objects do. None of these spontaneous processes are forbidden by energy conservation, they simply don’t happen. As Carter points out in his book Classical and Statistical Thermodynamics, the first law is general, useful, and simple but is ultimately unsatisfactory since it doesn’t distinguish between allowed and disallowed processes.
Obviously, spontaneous process are irreversible even if the precise logical connection between these two terms is not completely established. For example, if the converse is true then we can also conclude that all irreversible processes are spontaneous. This kind of question is more subtle that it might seem at first glance. We will have to content ourselves with looking at irreversible processes since irreversibility takes mathematical expression within the Clausius inequality.
To determine if a process is irreversible, one simply calculates the entropy change $\Delta S$ between the before and after states. If the change in entropy is positive, the process is irreversible and we conclude it will happen spontaneously in nature. Note that the specific path by which the final state is reached from the initial state is irrelevant since entropy is a state variable. Heat need not flow from a hotter to colder body in exactly the same way every time the same experiment is run for us to conclude that the process will operate irreversibly. This is the power of defining entropy as an exact differential (i.e., state variable) and using the change as the indicator.
To understand this further, we follow the example from Section 6.5 of Carter (which itself follows Fermi’s presentation in Sec. 13) where we imagine an irreversible process that transitions a system between two thermodynamic states $a \rightarrow b$ and a reversible process that carries the system back.
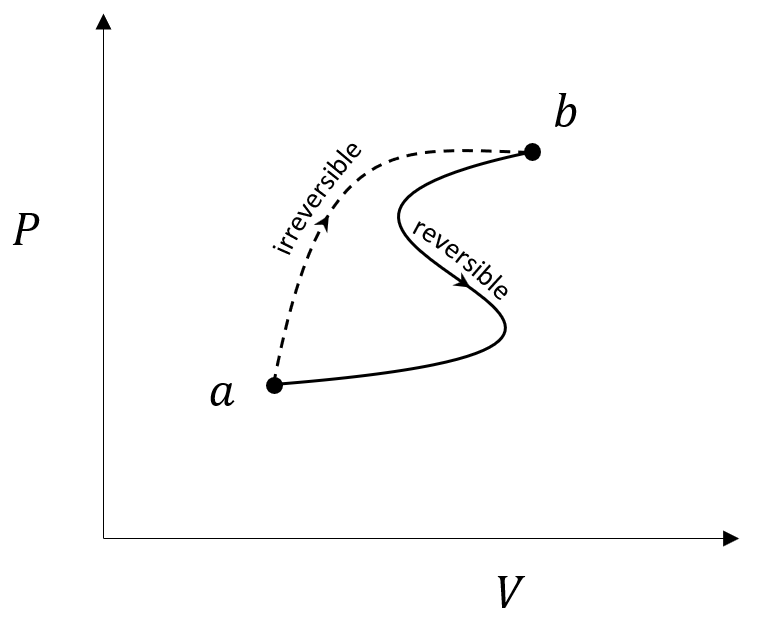
By the Clausius inequality
\[ \int_a^b \frac{ {\tilde d} Q}{T} + \int_b^a \frac{dQ_r}{T} \leq 0 \; . \]
Reversing the limits of the second integral (the reversible process) and rewriting the inequality gives
\[ \int_a^b \frac{{\tilde d} Q}{T} \leq \int_a^b \frac{dQ_r}{T} \; . \]
The reversible integral can be immediately written as the difference between the entropy values at the two states giving a final relation
\[ \Delta S = S_b – S_a \geq \int_a^b \frac{{\tilde d} Q}{T} \; \]
Now if the system is isolated, then $d\tilde Q = 0$, and we have that $\Delta S \geq 0$. This observation is the origin of the law that the entropy of the universe must always be increasing.
On a more modest scale, a nice simple example of the power of this method comes from General Chemistry, The Essential Concepts by Chang and Overby. In Example 18.2, they ask the student, using standard entropy values, to calculate the entropy change in two chemical reactions at $25 C$.
In the first chemical reaction
\[ CaCO_3(s) \rightarrow CaO(s) + CO_2(g) \; \]
has an entropy change of
\[ \Delta S^{\circ} = S^{\circ}(CaO) + S^{\circ}(CO_2) – S^{\circ}(CaCO_3)\\ = (39.8 + 213.6 – 92.9) J/(K \cdot mol) = 160.5 J/(K mol) \; , \]
while in the second chemical reaction
\[ N_2(g) + 3H_2(g) \rightarrow 2NH_3(g) \; \]
has an entropy change of
\[ \Delta S^{\circ} = 2 S^{\circ}(NH_3) – S^{\circ}(N_2) – 3 S^{\circ}(H_2)\\= (2 \cdot 193 – 192 – 3 \cdot 131) J/(K \cdot mol) = -199.0 J/(K mol) \; . \]
From these values, we would expect the first chemical reaction to occur spontaneously while the second would not.
The second innovation that entropy as an exact differential (i.e., state variable) provides is an incredibly useful rewrite of the first law of thermodynamics. The initial expression for the change in internal energy $U$ was expressed in terms of vague ‘inexact’ differentials as
\[ dU = {\tilde d} Q – \tilde{d}W \; ,\]
where, ${\tilde d} Q$ is the heat (positive if it flows into the system) and $\tilde{d}W$ is the work (positive if the system performs is). We needed to specifically account for heat flow and work performed at each and every step in the process, a nearly impossible task for reversible processes and almost certainly an impossible one for irreversible processes.
The introduction of the entropy provides the far more useful expression
\[ dU = TdS – PdV \; ,\]
where every term on the right-hand side is a state variable. This change is more than cosmetic as having only state variables frees us from having to pay attention to how a system evolves and allows us to focus only on the before and after conditions which is a far easier task.
To appreciate how this rewrite is possible, we follow the argument in Carter’s Section 6.8. Carter starts by noting that the Clausius inequality allows us to conclude that
\[ dS \geq \frac{ {\tilde d} Q}{T} \; . \]
The inequality can be removed by accounting for reversible and irreversible pieces separately so that
\[ TdS \equiv dQ_r = {\tilde d} Q + \epsilon \; , \]
where $\epsilon$ is some positive quantity and the $r$ subscript on $dQ_r$ reminds us that that is the quantity of heat into/out of the system during the reversible process. Substituting this into the first law gives
\[ dU = TdS – \epsilon – {\tilde d} W = T dS – ({\tilde d} W + \epsilon) \; .\]
The quantity in the parentheses is the amount of useful work done by the system plus the ‘tax’ associated with the system having to overcome dissipative forces. It is precisely the pressure work $PdV$ done by the system and so we arrive at
\[ dU = TdS – PdV \; .\]
without any loss of generality.
