Sadly Cannot
This post brings to a close, for the time being, the analysis of classical thermodynamics. It seems fitting to end with an example that sharpens much of what has been discussed over the past year or so. Such an example is given by Willis and Kirwan in their article The “Sadly Cannot” thermodynamic cycle. This two-stroke cycle is a thought-provoking model of a possible heat engine where a naive application of thermodynamics leads one astray. Finding one’s path back challenges one to think more carefully about what the terms of thermodynamics actually mean.
Their two-stroke engine consists of two simple thermodynamic processes connected together to form a cycle. A monatomic gas serves as a working fluid ($\gamma = C_P/C_V = 5/3$). Along the first leg of the cycle the gas decompresses from a volume $V_A$ to a volume $V_B$. The equation relating pressure and volume during this leg is the linear equation
\[ P = a V + b \; . \]
Along the second leg of the cycle, the gas is adiabatically compressed with the equation relating pressure and volume being
\[ P V^{\gamma} = constant \; . \]
The operating points $A$ and $B$, where the two legs connect, have pressures, volumes, and temperatures of $(P_A, V_A, T_A)$ and $(P_B, V_B, T_B)$, respectively. Two additional points are called out on the first leg. The first one, labeled $T_M$ is the point in the decompression leg where the temperature reaches a maximum. The second one, labeled $Q_R$ is the point where heat flow reverses from flowing into the system to flowing out. The name of the cycle, Sadly Cannot, is an homage to Sadi Carnot.
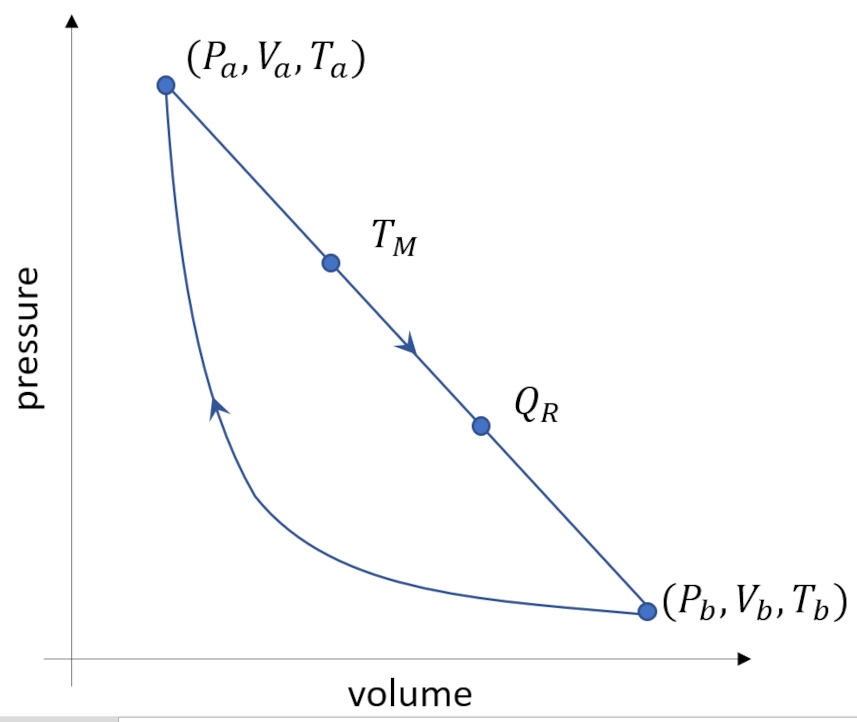
To see the magic of the Sadly Cannot cycle, Willis and Kirwan give a typical example. Given that $P_A = 32 Pa$, $V_A = 8 m^3$, $P_B = 1 Pa$, and $V_B = 64 m^3$, compare the thermal efficiency of this two-legged cycle to that of a Carnot cycle operating between the same two temperature extremes. Thermal efficiency, \ is defined as
\[ \epsilon = \frac{\textrm{work extracted}}{\textrm{heat supplied}} \; .\]
Let’s start by determining how much work is extracted. This value will be the sum of the signed areas lying below each curve. For the linear equation on the first leg, a simple calculation gives $a = (P_A – P_B)/(V_A – V_B) = -31/56 \, Pa/m^3$ and $b = (P_A – a V_A) = 255/7 \, Pa$. The work done by the gas along this leg is
\[ W_{A \rightarrow B} = \int_A^B P dV = \int_{V_A}^{V_B} (a V + b) dv = \left. \left(\frac{1}{2} a V^2 + b V\right) \right|^{V_A}_{V_B} = + 924 J\; .\]
The positive value of work is consistent with the expansion of the gas against the environment (e.g., a piston) and comes at the expense of some combination of reduced internal energy and heat exchange with the environment.
Since the second leg is, by construction, an adiabat, the work can be determined immediately from the first law since $\Delta U = Q_{B\rightarrow A} – W_{B\rightarrow A} = -W_{B\rightarrow A}$. Rather than performing an integral (which is easy enough but not illustrative), we can use the change in internal energy, which is directly related to the change in temperature by $\Delta U = 3/2nR(T_A – T_B)$, to calculate the work. We can eliminate temperature in favor of pressure and volume by using the equation of state to get $\delta U = 3/2(P_AV_A – P_BV_B) = -288 J$.
Thus the net work done during the cycle is $W_{net} = W_{A \rightarrow B} + W_{B \rightarrow A} = 636 J$.
We now need to calculate the heat transferred between our engine and its surroundings. We already used the fact that, by construction, $Q_{B\rightarrow A} = 0$ since the second leg is an adiabat. All we need is $Q_{A\rightarrow B}$. Here we may be tempted to again use the first law to arrive at the thermal efficiency of the engine arguing this way: Upon completing an entire circuit of the Sadly Cannot cycle, the gas is now back to the same thermodynamic state from which it started, thus the corresponding change in internal energy is $\Delta U_{net} = $. Applying the first law then gives
\[ \Delta U_{net} = 0 = Q_{net} – W_{net} \; , \]
or $Q_{net} = W_{net} = 636 J$. There is nothing intrinsically wrong with the calculation except that it doesn’t help us figure out what the thermal efficiency is and, if we use this value, we come up with the nonsensical value of $\epsilon =1$ in clear violation of one of the many equivalent ways of expressing the second law.
The next step involves answering two questions. The first is, what went wrong? The second is, what value should be used for the heat provided? In short, the answer to what went wrong is simply summarized by the following inequality:
\[ Q_{net} \neq Q_{supplied} \; .\]
The reason these two are not equal is that somewhere along leg 1 heat stops flowing into the system (i.e., being supplied) and starts flowing out (i.e., being shed). These two values of heat add to form $Q_{net}$, but only the value of $Q_{supplied}$ is used in computing the efficiency of our engine. The heat shed $Q_{shed}$ is energy given back to us by the process but it is energy with which we can do nothing useful until we feed it back into an engine (either this one or some other). To calculate $Q_{supplied}$ we need to integrate along leg 1 only to the point $Q_R$ where the heat reverses.
The heat along leg 1 is obtained from the first law again via
\[ Q = \int \Delta U + \int P dV + constant \; .\]
Since the internal energy only depends on temperature, we can, as above, use the equation of state to get
\[ U = \frac{3}{2} n R T = \frac{3}{2} P V = \frac{3}{2} \left( a V^2 + b V \right) \; . \]
Likewise, the work as a function of state is given by
\[ W = \int \left(a V + b\right) dV = \frac{a V^2}{2} + b V \; . \]
The heat as a function of state is then
\[ Q = 2 a V^2 + \frac{5}{2} b V + constant \; . \]
Setting $dQ/dV = 0$ and solving for V yields
\[ V_R = -\frac{5}{8} \frac{b}{a} = 1275/31 m^3 \; . \]
Plugging this value back into the linear equation relating pressure and volume gives a value of
\[ P_R = -3/8 b = 765/56 Pa \; . \]
The heat supplied is then
\[ Q_{supplied} = Q_R(P_R,V_R) – Q_A(P_A,V_A) \approx 1251 J \; , \]
yielding an efficiency of $\epsilon \approx 0.52$.
Calculating the efficiency of the corresponding Carnot cycle is also not a simple plug-and-chug. The maximum temperature occurs somewhere on leg 1 before the heat reversal. To find it, we recognize the $dU/dV=0$ applied to the expression for internal energy in terms of pressure and volume used above. Taking the derivative and solving for volume gives a value of $V_H = \frac{-b}{2a}$ at the corresponding pressure of $P_H = \frac{b}{2}$. The efficiency of the Carnot engine is
\[ \epsilon_{Carnot} = 1 – \frac{T_B}{T_H} = 1 – \frac{nRT_B}{nRT_H} = 1 – \frac{P_B V_B}{P_H V_H} \approx 0.89 \; .\]
In a companion piece entitled The “Sadly Cannot” Thermodynamic Cycle Revisited, Mills and Huston point out that these special points can be obtained by recognizing that the requirements that $dQ/dV=0$ for where the heat reverses and $dU/dV=0$ for maximum temperature mean that the point $Q_R$ falls on an adiabat (since no heat is flowing at that point) and the point $T_M$ on an isotherm (since the temperature is not changing at the point). Along the adiabat $P V^{\gamma} = constant$ and the implicit derivative from this equation can be connected to the explicit linear equation to arrive at the same values for $V_R$ and $P_R$. Likewise, the same process is used along the isotherm with the only change being to use $PV = constant$.
It is rare to find such a satisfying example anywhere in physics as the Sadly Cannot cycle is. Well done, Willis and Kirwan.
