Kinetic Theory 1 – The Basics
Last month’s post marked a logical end to the study of classical thermodynamics. This month’s post begins the transition from thermodynamics to statistical mechanics by giving a simple treatment of the kinetic theory of gases. While the mathematical and theoretical sophistication of kinetic theory is quite high, this introductory post will confine itself to an elementary treatment following Physics by Halliday and Resnick but with additional departure points identified. The results that follow should serve as a baseline for a more realistic presentation to follow.
The aim of kinetic theory is to establish the properties of a gas, most notably the ideal gas law, in strictly mechanical terms. The three thermodynamic variables of volume, $V$, pressure, $P$, and temperature, $T$, have their ultimate definition in terms of the microscopic movement of the gas molecules. The volume occupied by the gas should be obviously connected to the density of the gas, but it may be somewhat harder to understand that pressure is a manifestation of the momentum imparted to nearby objects through the collision of the gas with them. The connection between the temperature and the average kinetic energy per molecule should be even more removed.
Since the ideal gas law finds applications in a variety of physical scenarios from the modeling of galaxies and stars to more terrestrial applications in internal combustion and steam engines and weather and atmospheric modeling, the success of the mechanistic approach of kinetic theory was one of the great triumphs of 19th century physics. In unearthing these connections we will assume that the ideal gas law is given as
\[ P V = n R T = N k_B T \; , \]
where $n$ is the number of moles and $R$ is the ideal gas constant, which can also be expressed in terms of the Boltzmann constant $k_B$ and Avogadro’s number $N_A$ as $R = k_B N_A$.
The typical textbook story starts with looking a single particle moving within a cubical enclosure of side length $L$. The confinement to a single particle is not as radical as it may seem at first since this arrangement is logically equivalent to having $N$ particles in the box that don’t interact with each other (i.e., no collisions). This latter assumption is easy to relax after the derivation and it will be addressed again below.
We envision this single particle to have a mass $m$ and initial velocity ${\vec v}_I = (v_x,v_y,v_z)$. Let us suppose that the particle is approaching the right-most face perpendicular to the $x$-axis.
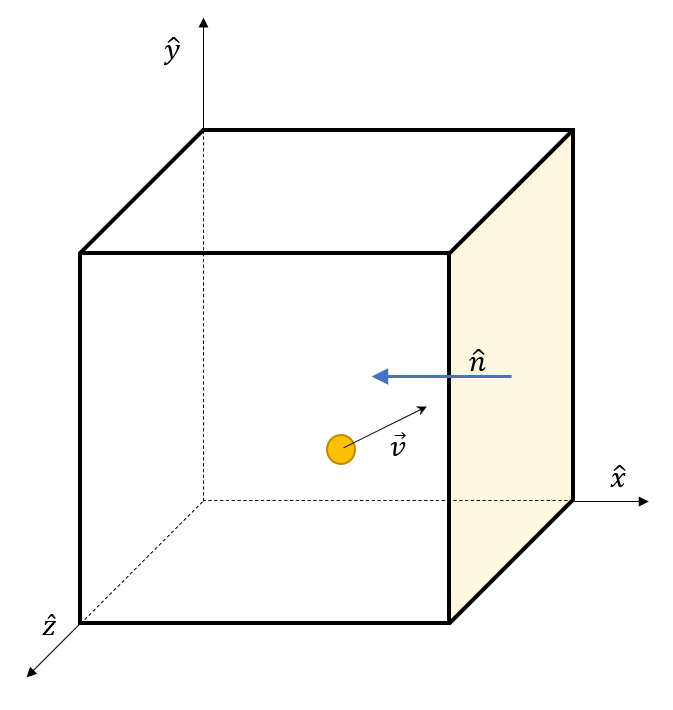
If the particle elastically collides with the wall, its $x$-component of velocity is negated leaving a final velocity ${\vec v}_F = (-v_x,v_y,v_z)$. The change in particle momentum during the collision is
\[ {\vec p}_{F} – {\vec p}_{I} = m {\vec v}_F – m {\vec v}_I = (-2 m v_x ,0,0) \; .\]
In response, the momentum transferred to the wall is
\[ \Delta {\vec p} = (2 m v_x,0,0) \; . \]
We now follow as the particle strikes the opposite wall, rebounds, and then again strikes the first wall. The time it takes for this round trip across the enclosure is
\[ \Delta t = \frac{2 L}{v_x} \; , \]
independent of whether or not is strikes the other faces with unit normals not along the $x$-axis. The force this particle exerts on the right-most wall of the container is the change in momentum imparted at each collision divided the time between collisions and is given by
\[ {\vec F} = \frac{\Delta {\vec p}}{\Delta t} = \frac{(2m v_x,0,0)}{2 L / v_x} = \left( \frac{m v_x^2}{L} \right) \; . \]
With the result for a single particle in hand, we can now imagine the box now filled with $N$ particles each with their own particular value for the $x$-component of the velocity, which we will track with an index: $v_{xi}$. The pressure due to all of these particles is then the ratio of the total force to the area of the face and is given by
\[ P = \frac{F_x}{L^2} = \frac{m v_{x1}^2/L + m v_{x2}^2/L + \cdots m v_{xN}^2/L }{L^2} \\ = \frac{m}{L^3} \left( v_{x1}^2 + v_{x2}^2 + \cdots v_{xN}^2 \right) \; .\]
Multiplying the numerator and denominator of the last expression by $N$ gives the pressure in terms of the average $x$-component of the velocity as
\[ P = \frac{m N}{L^3} ( v_x^2 )_{ave} \; . \]
We can express the average $x$-component of the velocity in terms of the average of the speed by first noting that by definition $v^2 = v_x^2 + v_y^2 + v_z^2$ and that since there is nothing special about the $x$ direction (i.e., there is rotational symmetry), the $y$ and $z$ directions must also have the same value. Combining these two ideas we get that
\[ (v^2_x)_{ave} = \frac{(v^2)_{ave}}{3} \; .\]
Since $L^3 = V$, we can rewrite the pressure as
\[ P = \frac{m N}{3 V} (v^2)_{ave} \; .\]
This last this expression for pressure can be directly compared with the thermodynamic equation of state giving
\[ \frac{N k_B T}{V} = P = \frac{N m v^2_{rms}}{3 V} \; . \]
Eliminating common factors and renaming the average speed, as is traditional, as the root-mean-square speed we get
\[ T = \frac{m N v_{rms}^2 }{3 k_b} = \frac{2}{3} \frac{KE_{rms}}{k_b} \; .\]
The physical meaning we attach to this expression is that the temperature perceived by a thermometer is two thirds of the kinetic energy of the gas moving at $v_{rms}$ scaled by the Boltzmann constant.
Since we can directly measure temperature much more easily than we can measure molecular speeds, the more common way of presenting this relationship is to express $v_{rms}$ in terms of temperature as
\[ v_{rms} = \sqrt{ \frac{3 R T}{M} } \; ,\]
where the macroscopic parameters of the ideal gas constant $R = k_B N_A$ and molar mass $M$.
This connection between temperature and kinetic energy is profound but is subject to several questions.
First, what modifications result if inter-particle collisions are accounted for? It turns out that no modifications are actually needed since the action of a collision will be to switch velocity components between the particles involved in the collision due to the conservation of momentum. Since we imagine that a whole distribution of speeds is present for each component the statistical average figuring into the pressure remains unchanged. This argument can also be found in Halliday and Resnick’s first chapter on Kinetic Theory.
Second, and more importantly, what modifications result if the collisions (inter-particle or particle-with-wall or both) are inelastic? The obvious interpretation is that energy is lost or gained as heat but the clear signposts pointing to this conclusion are not even touched upon in an elementary presentation and aren’t obvious in the simplistic treatment above. This is the operative question because it carries in its train a host of related questions such as: what if the collision create new particles? what if the collision is mediated by a field? what if the collisions are overlaid with a long-range force? and so on. No doubt, this is where the conservation of momentum plays a starring role but exactly how remains to be seen as we work our way through kinetic theory.
Next month, we’ll look at how the individual particle speed are distributed around $v_{rms}$ by deriving the famous Maxwell-Boltzmann distribution.
