Kinetic Theory 5 – Mean Free Path in the Atmosphere
In the last post, we established that the mean free path of a particle, the average distance that the particle travels before suffering a collision with another particle is given by
\[ \lambda = \frac{1}{(N_{rel}/N_{avg}) \pi d^2 n} \; , \]
where $d$ is the characteristic diameter of the particle (i.e., diameter of a bounding sphere) and $n$ is the number density, which depends on temperature and pressure through the ideal gas law . The factor $N_{rel}/N_{avg}$ is a numerical factor that represents the ratio between the relative speed between the two particles and the average speed of a particle in the gas. It should be remembered that not all authors agree on which of these statistically significant speeds – mean, most probable, and RMS – should be used in computing the mean free path, so the ratio $N_{rel}/N_{avg}$ can take on values of $\sqrt{2}$, $\sqrt{8/\pi}$, and $\sqrt{3}$, respectively. While it is important to have rigor and clarity in the analysis and it would be ideal for everyone to agree on the expression, there is little physical impact in choosing one over the other as there is currently no way to independently measure the characteristic diameter of the particle. Since it is the product of $d^2 (N_{rel}/N_{avg})$ that matters, adjustments to one can be compensated with an appropriate adjustment to the other. As a result, we’ll take as given the more common value for $ N_{rel}/N_{avg} = \sqrt{2}$.
It is useful to get some sense of the numbers involved for the mean free path in typical terrestrial situations. To that end, we’ll look at the value of the mean free path for air as a function of altitude from sea level upwards using a crude scale height model of the atmospheric density (see also Kinetic Theory 2 – Maxwell-Boltzmann Distribution).
Atmospheric density in a scale height model is given by
\[ n = n_0 exp \left( – \frac{m g z}{k_B T} \right) \equiv n_0 exp \left( – \frac{z}{H} \right) \; , \]
where $n_0$ is the density at sea level, $z$ is the height in the atmosphere, $H = m g/k_b T$ is the scale height parameter that only depends on the average molecular mass, $m$, of the atmosphere, which is the weighted average mass of molecular nitrogen and oxygen (assumed to be the only components in this abbreviated model) and the temperature $T$; $k_B = 1.38 \times 10^{-23} \, J/K$ being Boltzmann’s constant and $g = 9.8 \, m/s^2$ being the standard gravitational acceleration at sea level. This exponential form results by assuming that the temperature is constant. While this assumption is rather poor in fine details, we will use it due to its extreme simplicity.
To get the molecular mass of the air, start first with the molar mass of molecular nitrogen $N_2$ and molecular oxygen $O_2$, whose values are $28 \, amu$ and $32 \, amu$, respectively. Using the value Avogadro’s number $N_A = 6.022 \times 10^{23}$, the molecular masses (in kilograms) for each of these molecules are: $M_{N_2} = 4.65 \times 10^{-26} \, kg$ and $M_{O_2} = 5.31 \times 10^{-26} \, kg$. Combining these according to their relative occurrence in atmosphere ($N_2$ at 78
\[ \frac{H}{T} = 29.5 \, m/K \; .\]
Assuming that the pressure at sea level is one atmosphere ($P_0 = 101325 \, Pa$), the density at sea level is then obtained from the ideal gas law as
\[ n_0 = \frac{P_0}{k_B T} \; , \]
which numerically has the value $n_0 = 2.45 \times 10^{25}/m^3$.
The only remaining piece is the molecular diameter of air which is again a weighted average of the molecular diameter of $N_2$ and $O_2$ which we take to be $364 \, pm$ and $346 \, pm$, respectively, based on the values listed in Wikipedia for kinetic diameters. The resulting weighted average gives a molecular diameter of $360 \, pm$ for air.
At a temperature of $T = 27 \, C = 300 \, K$, the mean free path at sea level is $\lambda = 70.9 \, nm$, which, while very small, is still some 200 times larger than the molecular diameter of air. This means that the assumption underlying kinetic theory – that the particles only interact via direct collision and that those collision take place pairwise – is well supported.
A related but equally important parameter is the collision time. The collision time, which is the average time between any two collisions, is related to the mean free path by
\[ \tau = \frac{\lambda}{v_{avg}} \; , \]
where the average speed is given by $v_{avg} = \sqrt{8 k_B T/\pi m}$. For the $T = 300 \, K$ case above, the corresponding collision time is $\tau = 150 \, ps$. This value will become more important latter in understanding the collision operator in the Boltzmann equation.
Of course, we can expand these results to various altitudes above the Earth using our scale height model. The following plot shows the variation in mean free path as a function of altitude for various temperatures.
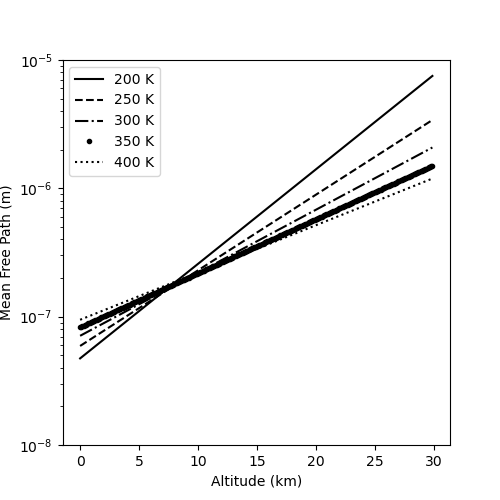
To get an idea of the accuracy of this model, one can compare its prediction for the mean free path to those from U.S. Standard Atmosphere. At an altitude of $11 \, km$, the standard atmosphere lists the pressure as $P_{11} = 22632.1 \, Pa$ with a corresponding temperature of $T_{11} = 216.65 \, K$. Using the ideal gas law, the corresponding number density is $n_{11} = 7.57 \times 10^24 /m^3$ resulting in a mean free path $\lambda_{11} = 2.3 \times 10^-7 \, m \approx 0.2 \mu m$, which is roughly the value predicted by the various models. At $32 \, km$ a similar computation yields $\lambda_{32} \approx 6 \, \mu m$, which agrees with a scale heigh model to within a factor of 10. Finally, it is interesting to note that at an altitude of $71 \, km$ (the last fully-listed value) the mean free path is approximately $\lambda_{71} \approx 1 mm$, which makes it on the scale easily seen by the eye (if the eye could actually see the molecule).
