Kinetic Theory 6 – Transport Coefficients 1
This month’s and the next two month’s blogs mostly follow Chapter 12 in Fundamentals of Statistical and Thermal Physics by Frederick Reif with some occasional input from (and comment on) other resources. The primary aim of this post is to show how a very simplistic theory can put the mean free path to use in non-equilibrium situations to make a connection between macroscopically observing bulk transport and the underlying microscopic mechanical motions.
The three cases we will look at are the macroscopic effects of: 1) self-diffusion, which involves the transport of mass, 2) fluid viscosity, which involves the transport of momentum, and 3) heat conduction, which involves the transport of energy. This order follows the common order used in continuum mechanics for following bulk effect and the corresponding equations in that context are: 1) mass continuity, 2) Cauchy momentum equation, and 3) energy equation.
It is important to stress, that each of these computations is done without regard to the velocity distributions beyond what has already been employed to calculate the mean speed ${\bar V}$ and the mean free path $\lambda$. Thus, the results that are obtained need to consumed with some care. The functional dependence of the macroscopic terms on the underlying mechanical analogs is expected to be correct by the overall numerical factor will likely be off by up to a factor of 3 or 4. This situation is very similar to those discussed in previous blogs concerning which of the statistically significant speeds (most probable, mean, or RMS) should be used in any computation.
This blog will focus on self-diffusion as the model problem since the other two (viscosity and thermal) follow in much the same way.
Self Diffusion
In Reif’s treatment of self-diffusion, he considers a substance consisting of similar molecules where some subset of them is tagged so that they are observationally distinguishable but (though he doesn’t quite say this) their distinguishability doesn’t affect their mechanical motion. The mechanism he proffers is that they emit some sort of nuclear radiation that, ostensibly, doesn’t change the mass, but a fluorescence, for example by Raman spectroscopy, might have been a better choice. Regardless, it seems that he is trying to avoid the situation in which the mass concentration $\rho_m$ varies by constructing a scenario in which only the number concentration $n$ does, ostensibly to avoid bulk motion due to macroscopic flows (i.e., the pressure is uniform).
Once the molecules have been tagged, he constructs a scenario in which the number density is uniform in the $x$ and $y$ at any fixed value of $z$ but which varies as $z$ does. As a result, the number density depends on position and time so that $n = n(z,t)$. There is now a corresponding number density flux ${\vec J} = J_z(z,t) {\hat z}$ in the $z$-direction. Macroscopically, we assume that since $J_z$ is non-zero when there are differences in the number density, then a linear relationship of the form
\[ J_z = – D \frac{\partial n}{\partial z} \; , \]
will be adequate provided the gradients are small in some sense. This relationship is a specific example of Fick’s law
\[ {\vec J} = – D \nabla n \; \]
and $D$ is the self-diffusion constant. Support for so naming $D$ comes from the fact that if we take the divergence of both side of Fick’s law and the use number continuity equation
\[ \frac{\partial n}{\partial t} + \nabla \cdot {\vec J} = 0 \; \]
to eliminate $\nabla \cdot {\vec J}$ we get
\[ -\frac{\partial n}{\partial t} = -D \nabla^2 n \; , \]
which is the classical diffusion equation. This classical form, which is well-known, depends on the assumption that $D$ has no spatial dependence; an assumption that is usually stated but not justified. The elementary transport theory that Reif presents gives a rationale for this assumption and a mechanism to explore for when and how it might break down.
Now consider any plane whose normal is parallel to ${\hat z}$ in between the boundaries with the least and the most concentration of the tagged molecules
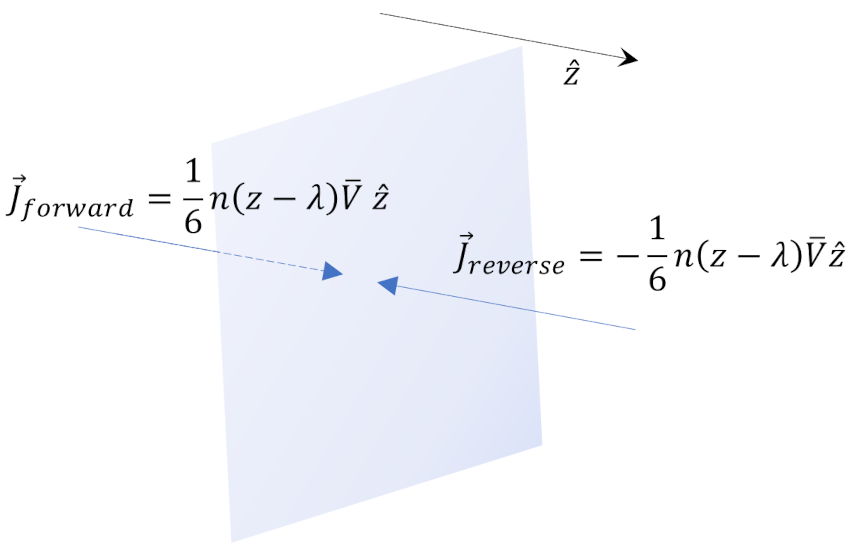
Reif argues that $1/6$ of the particles are heading in any of the 6 cardinal direction of $\pm {\hat x}$, $\pm {\hat y}$, and $\pm {\hat z}$. The forward and reverse number density fluxes, relative to crossing the plane in the +$z$-direction, are given by
\[ {vec J}_{forward} = \frac{1}{6} n(z-\lambda) {\bar V} {\hat z} \; \]
and
\[ {\vec J}_{reverse} = -\frac{1}{6} n(z + \lambda) {\bar V}{\hat z} \; .\]
Note that the mean free path comes in by linking the flux crossing the plane with the number density at a point $z \pm \lambda$ away from which represents that flux originates. In other words, the molecules that are crossing the plane at $z$ are carrying information from a region one mean free path away, since they will, on average, have suffered no collisions (i.e., interactions) in their travels from that region.
The $z$-component of the number density flux is then
\[ J_z(z) {\hat z} = {\vec J}_{forward} + {\vec J}_{reverse} \; \]
or
\[ J_z(z) = \frac{1}{6} {\bar V} \left[ n(z-\lambda) – n(z + \lambda) \right] = -\frac{1}{3} \lambda {\bar V} \frac{\partial n}{\partial z} \; .\]
Comparing the macroscopic expression arising from Fick’s law to this one we arrive at
\[ D = \frac{1}{3} \lambda {\bar V} \; .\] It is interesting to note that in both Kittel’s and Kromer’s book Thermal Physics and in Ashley Carter’s Classical and Statistical Thermodynamics one finds more complicated arguments about averaging over directions and distances to get the leading numerical factor of $1/3$ in the above relation. I find each of the arguments personally difficult to follow; particularly problematic is that there is a strong linkage between the mean speed, the direction of motion, and the mean free path that leads to a ‘double average’ that ends up resulting in the same wrong numerical factor out front. As discussed above, the value of $1/3$ can be expected to be good only to a factors on the order of unity. Reif’s presentation, which simply asserts an intuitive $1/6$ for each of the $6$ cardinal direction, seems far more understandable and concise.
