Kinetic Theory 8 – Transport Coefficients 3
In the last two blog posts, we’ve related the macroscopic, phenomenological parameters of self-diffusion $D$ and viscosity $\mu$ to the underlying kinetic theory parameters of mean free path and mean speed. In this blog, we complete this exploration by looking at the final form of transport: thermal conductivity. As in similar posts, this one follows Reif Chapter 12.
Thermal Conductivity
In this case, the temperature is not uniform throughout a system. The typical case is shown below for $T_2 > T_1$, where heat flows from the top plate to the bottom one carried by the heat flux ${\vec q}$.
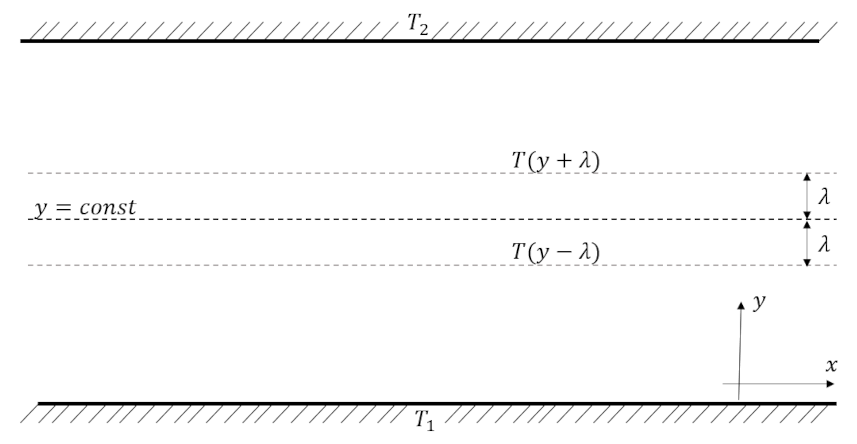
Macroscopically, ${\vec q}$ depends on the temperature gradient and, as is usual, a reasonable approach is to assume a linear relationship given by
\[ q_y = – K \frac{\partial T}{\partial y} \; , \]
where $q_y$ is the only non-zero component of the heat flux.
Microscopically, we focus on a single plane falling somewhere between the plates whose normal is along the positive $y$ direction. On average, 1/6 of the molecules will be crossing the plane moving in the upwards direction and 1/6 will be crossing in the downwards direction. Each of these populations will be carrying a different average energy ${\mathcal e}$ since they represent the conditions one mean free path away from the plane on either the lower or upper side, respectively.
The $y$-component of the heat flux can then be expressed as
\[ q_y = \frac{1}{6} n {\bar v} \left[ {\mathcal e} (y – \lambda) – {\mathcal e} (y + \lambda) \right] \; , \]
where $n$ is the number density, ${\bar v}$ is the mean speed, and $\lambda$ is the mean free path.
Expanding this expression in Taylor series in $\lambda$ and throwing away the higher order terms yields
\[ q_y = – \frac{1}{3} n {\bar v} \frac{\partial {\mathcal e}}{\partial y} \lambda \; . \]
To relate the internal energy gradient to the temperature we first recall that the internal energy depends on temperature and we then use the chain rule to rewrite the heat flux expression as
\[ q_y = – \frac{1}{3} n {\bar v} \frac{\partial {\mathcal e}}{\partial T} \frac{\partial T}{\partial y} \lambda \; . \]
Following the first law of thermodynamics $dE = T dS – P dV$, we can re-express the first partial derivative as the heat capacity $c$ per molecule and we finally arrive at
\[ q_y = – \frac{1}{3} n {\bar v} c \lambda \frac{\partial T}{\partial y} \; . \]
Comparing this with the macroscopic expression gives
\[ K = \frac{1}{3} n {\bar v} c \lambda = n c D \; . \]
As was noted with the analysis of viscosity, these types of results lead to the correct functional dependence, but one should take the leading numeric factor with a grain of salt. In addition, we’ll remind the reader that other authors get the $1/3$ factor using quite different ways of ‘averaging’ across the populations.
One consequence of this functional dependence is that the heat conduction of a gas is independent (at least over a very broad range of physical scenarios) of the pressure of the gas. At first glance, this may seem entirely counterintuitive as the denser a gas becomes the more thermally conductive one might expect it to be because there is more material to carry the thermal energy. However, assuming hard sphere collisions, the expression for the mean free path is $\lambda = 1/\sqrt{2} n d^2$ and when substituted into the above expression yields an expression independent of density (i.e., pressure):
\[ K = \frac{1}{3} n {\bar v} C_V \frac{1}{\sqrt{2} n d^2} = \frac{1}{3} \frac{ {\bar v} C_V }{d^2} \; .\]
The absence of density in the above expression may challenge the well-known idea that a vacuum flask is able to keep material inside essentially thermally isolated from the environment. These two observations are reconciled by noting that when a high vacuum exists within the inner and outer flasks, the mean free path is larger than the physical dimensions of the container, and the above assumed form of the $\lambda \propto 1/n$ no longer holds.
An additional check as to the correctness of this analysis can be made by comparing back to the expression for viscosity ($M$ is the molecular mass)
\[ \mu = \frac{1}{3} M n {\bar V} \lambda = M n D \; , \]
derived in the previous post. Taking the ratio between these two expressions allows us to make a tangible, macroscopic test of this theory, since our analysis predicts that
\[ \frac{K}{\mu} = \frac{c}{M} = \frac{C_V}{m_{mol}} \; ,\]
where $C_V$ is the heat capacity at constant volume and $m_{mol}$ is the molar mass of the gas.
Reif cites that actual measurements of this relationship have the coefficient out from departing from unity by values ranging from 1.3 to 2.5, which is excellent agreement given the myriad of physical details that have been omitted from the model.
Finally, the functional dependence of the thermal conductivity as a function of temperature can be determined by noting that the mean speed ${\bar v}$ is proportional to the square root of temperature leading to $K \propto T^{1/2}$. As discussed in the previous post, the assumption of hard sphere scattering is only an approximation and the molecular interactions depend on speed of the scattering objects relative to each other. This introduces a dependence in the thermal conductivity making it increase with increasing temperature with a greater exponent, perhaps as much as $K \propto T^{0.7}$ or $T^{0.8}$.
