Monthly Archive: July 2015

Last week’s column examined the use of the Lie series to the problem of the pendulum. As a model in classical mechanics, the pendulum is interesting since it is essentially nonlinear with a well-known analytic solution in terms of elliptic integrals. By essentially nonlinear, I mean that the problem doesn’t possess a nonlinear transformation that permits the differential equation to be recast as a linear problem, like is possible in the Kepler problem.

The comparison of the ‘exact’ solution in terms of elliptic integrals to the Lie series is very difficult. Expansions of the exact solution in power series in very complex due to both the Jacobi $$sn$$ function and the $$\sin^{-1}$$ in the analytic form. In contrast, the Lie series, which essentially generates the Taylor series in a compact, self-interative way, seems to not have any easily identified correspondence.

As a result, it seemed prudent to look at the numerical solutions of both approaches – exact and Lie series. Numerical integration using a Runge-Kutta integration scheme acts as a stand in for the exact elliptical integral solution. WxMaxima served as the tool to tackle this comparison as it does a fairly competent job of mixing symbolic and numerical processing (although it would be nice to try out a mix of numpy, scipy, and sympy in a Jupyter shell – perhaps sometime in the future).

To start, the $$D = \omega_0 \partial_{\theta_0} – g \sin(\theta_0) \partial_{\omega_0} $$ was defined as

D_pen(arg) := w*diff(arg,T) - g*sin(T)*diff(arg,w);

Two things are worth noting. First, the operator $$D$$ is given a decoration in the program so that, during testing, other functional forms could be used without clash. In particular, the use of $$D = \omega_0 \partial_{\theta_0} – g \theta_0 \partial_{\omega_0}$$ was especially helpful since the Lie expansion of the simple harmonic operator corresponds to the regular expansion of $$\sin$$ and $$\cos$$ and so is easy to check that the algorithm is correct. Second, note that the subscript reminding us that the operator acts upon the initial conditions has been suppressed. In some sense, it is not needed except as a reminder of that particular fact and, with that notion understood, it can be dropped.

The next order of business is to define a function that allows the formation of the Lie series based on $$D$$ to order $$n$$. This is accomplished using

L(order,D) := block([ret,temp],
                     ret  : T,
                     temp : T,
                     for n : 1 step 1 thru order do
                         block([],
                               temp : D(temp),
                               ret  : ret + t^n/n!*temp),
                     ret)$

As a test, L(4,D_pen) yields

\[ {{t^4\,\left(g^2\,\cos T\,\sin T+g\,w^2\,\sin T\right)}\over{24}}-{{g\,t^2\,\sin T}\over{2}}-{{g\,t^3\,w\,\cos T}\over{6}}+T+t\,w \; ,\]

which, up to a cosmetic change in notation, is seen to be the same expression as was derived last week.

The final function needed to complete the analysis is one that converts the symbolic form to numeric form for easy plotting and numerical comparisons. That function is defined as

Q(order,D,parms) := block([Lie],
                  Lie : L(order,D),
                  Lie : ev(Lie,parms));

What $$Q$$ does is to first retrieve the expression of the Lie series for a user-specified order and $$D$$ operator and then to evaluate that expression numerically using the $$ev$$ function built into Maxima. The list $$params$$ provides a convenient way to piggyback the appropriate parameters that match the problem at hand. These parameters include the numerical values of the initial conditions, any physical constants (e.g. $$g$$ in the problem of the pendulum), and the specific time at which the evaluation is to take place.

The next step is the solve the pendulum problem using a Runge Kutta and to assume that the resulting solution is close enough to the exact solution to be of use. The steps for this are fairly straightforward but a disciplined approach helps to remember the order of the arguments in the syntax.

The first step is to load the dynamics package using:

load("dynamics")

The second step is to define the physical constant for $$g$$

G : 10

(note that the symbol $$G$$ is chosen for the numerical value of $$g$$ to allow the later to stay as a symbolic quantity).

Next define the differential equations to be solved

dT_dt   : w;
dw_dt   : -G*sin(T);
my_odes : [dT_dt, dw_dt];

the names of the dynamic variables and their initial conditions

var_names : [T,w];
T0  : 2;
w0  : 0;
ICs : [T0,w0];

and the time mesh used for the integration

t_var   : t;
t_start : 0;
t_stop  : 3;
t_step  : 0.1;
t_domain: [t_var, t_start, t_stop, t_step];

Structured in this way, the call to the Runge Kutta integrator is nice and clean

Z : rk(my_odes, var_names, ICs, t_domain)$

The data structure $$Z$$ is a list of lists. Each of the sub-lists has three elements corresponding to the values of $$[t,\theta,\omega]$$ and the outside list has $$n$$ elements where $$n$$ is number of time points in the mesh defined above.

To make plots of the data requires massaging the results in a list of lists with only two elements (either $$[t,\theta]$$ or $$[t,\omega]$$) for use in a discrete plot. In addition, for proper comparison, similar lists are needed for the simple harmonic oscillator (as a linear problem baseline) and for different orders of the Lie series.

The built-in command makelist is the workhorse here with the desired list of lists being specified as

pen   : makelist( [Z[n][1],Z[n][2]],n,1,31)$
SHO   : makelist([(n-1)*0.1,2*cos(sqrt(10.0)*(n-1)*0.1)],n,1,31)$
Lie5  : makelist([(n-1)*0.1,Q(5,D_pen,[T=2.0,w=0.0,g=10.0,t=(n-1)*0.1])],n,1,31)$
Lie10 : makelist([(n-1)*0.1,Q(10,D_pen,[T=2.0,w=0.0,g=10.0,t=(n-1)*0.1])],n,1,31)$

These lists are then displayed using

wxplot2d([[discrete,pen],[discrete,SHO],[discrete,Lie5],[discrete,Lie10]],[x,0,1],[y,-2,2],[legend,"Pendulum","SHO","Lie5","Lie10"],[xlabel,"time"],[ylabel,"theta"]);

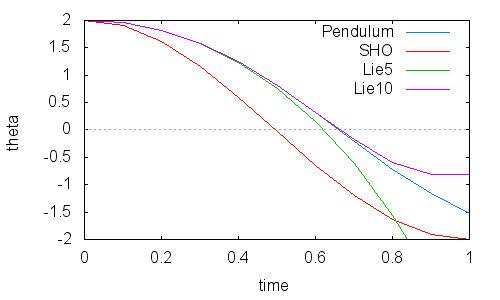
The resulting plot is

Several observations follow immediately from a careful inspection of this plot. First, the nonlinearity of the pendulum is quite obvious as the motion (blue trace) quickly departs from the corresponding motion from the simple harmonic oscillator (red trace). The Lie series capture this departure reasonable well as both the 5th and 10th order behavior (green and purple traces) sits on top of the exact solution for times less than 0.4. After this time, the 5th order begins diverging. The 10th order Lie series stays relatively close until a time of 0.7 where it too begins to diverge. Neither one makes it even a half a period, which is a disappointing observation. Clearly, while the Lie series is universal it is applicability it also seems to be universal in its limited range of convergence about the exact solution.

For this go around with the Lie series, I thought it would be interesting to experiment with a problem quite unfamiliar to me – namely the full nonlinear pendulum equation. The approach here is two-fold. First, the classical computation for this key problem is presented. For this part, I use Lowenstein’s discussion in the book ‘Essentials of Hamiltonian Dynamics’ as a model. In the second part, I apply the Lie series to the system to see how well the generated expansion matches the classical result. The classical result requires a lot of familiarity with special functions and some clever and unmotivated substitutions. The hope here is that the brute force and straightforward method provided by the Lie series will be accurate enough when compared with the classical result to make it attractive.

Now to set the notation and conventions, consider the following figure of the pendulum.

The angle $$\theta$$ from the vertical is clearly the only relevant degree of freedom. The pendulum bob of mass $$m$$ possesses a kinetic energy of

\[ K = \frac{1}{2} m R^2 \dot \theta^2 \; ,\]

where $$R$$ is the length of the pendulum. As denoted in the figure, the zero of the potential energy is taken when the bob is horizontal so that $$\theta = \frac{\pi}{2}$$. The potential energy function is then

\[ U = – m g R \cos \theta \; ,\]

For convenience in what follows, set $$m = 1$$ and $$R = 1$$. The Lagrangian of the system is then

\[ L(\theta,\dot \theta) = \frac{1}{2} \dot \theta ^2 + g \cos \theta \]

with the corresponding Euler-Lagrange equations of

\[ \ddot \theta + g \sin \theta = 0 \; .\]

The conjugate momentum

\[ p_{\theta} = \frac{\partial L}{\partial \dot \theta} = \dot \theta \]

becomes the new independent variable in the system when we switch to the Hamiltonian

\[ H(\theta,p_{\theta}) = \frac{p_{\theta}^2}{2} – g \cos \theta \; .\]

Since $$H(\theta,p_{\theta})$$ has no explicit time dependence,

\[ \frac{d H}{dt} = \frac{\partial H}{\partial t} = 0 \; ,\]

it is a conserved quantity that is the total energy.

With the conservation firmly in hand, we can eliminate the conjugate momentum in favor of the generalized velocity to get the energy equation

\[ \frac{1}{2} \dot \theta ^2 – g \cos \theta = E \; .\]

At this point, the special function gymnastics begin with the substitutions

\[ z = \frac{1}{k} sin \left( \frac{\theta}{2} \right) \]
and
\[ k = \sqrt{ \frac{E + g}{2 g} } \; ,\]

which bring the energy equation into the form

\[ \dot z ^2 = g(1-k^2 z^2) (1 – z^2) \; .\]

Solving this for $$dt$$ gives

\[ dt = \frac{dz}{ \sqrt{ g(1-k^2 z^2) (1 – z^2) } } \]

which integrates to

\[t – t_0 = \frac{1}{\sqrt{g}} \int_0^z \frac{d \zeta}{\sqrt{ g(1-k^2 \zeta^2) (1 – \zeta^2)}} \]

The integral on the right-hand side is important enough to have its own name – it is an elliptic integral of the first kind and its solutions are defined as

\[ F(sin^{-1} z|k^2) \equiv \frac{1}{\sqrt{g}} \int_0^z \frac{d \zeta}{\sqrt{ g(1-k^2 \zeta^2) (1 – \zeta^2) }}\]

By construction, $$k^2 \in [0,1)$$ corresponds to the librating situation where the bob has only enough energy to move to and fro without spinning about it point of rotation. The classical solution for $$z$$ is compactly written as

\[ z = sn(\sqrt{g}(t-t_0),k^2) \]

where $$sn$$ is the Jacobi elliptic integral. Inverting the defining relation between $$z$$ and $$\theta$$ gives the final solution as

\[ \theta(t) = 2 \sin^{-1}\left(k sn(\sqrt{g}t,k^2) \right) \; .\]

Understanding how to mine information from these expressions requires a fairly sophisticated understanding of the elliptical integrals, which, while important for this key problem, don’t translate universally.

To apply the Lie series, rewrite the equations of motion in state space form

\[ \frac{d}{dt} \left[ \begin{array}{c} \theta \\ \omega \end{array} \right] = \left[ \begin{array}{c} \omega \\ – g \sin \theta \end{array} \right] \]

from which is read the differential operator

\[ D = \omega_0 \partial_{\theta_0} – g \sin \theta_0 \partial_{\omega_0} \; .\]

The solution to the problem is then given by
\[ L[\theta_0] = e^{(t-t_0)D} \theta_0 \; .\]

As is usually the case, the Lie series is tractable to hand computations for the first few terms. The relevant operations with $$D$$ are:

\[ D \theta_0 = \omega_0 \; ,\]

\[ D^2 \theta_0 = – g \sin \theta_0 \; , \]

\[ D^3 \theta_0 = – g \omega_0 \cos \theta_0 \; , \]

and

\[ D^4 \theta_0 = g^2 \cos \theta_0 \sin \theta_0 + g \omega_0^2 \sin \theta_0 \; .\]

The resulting Lie series is quite unwieldy resulting in

\[ L[\theta_0] = \theta_0 – g \frac{(t-t_0)^2}{2!} \sin \theta_0 + \left( (t-t_0) – g \frac{(t-t_0)^3}{3!} \cos \theta_0 \right) \omega_0 \\ + \frac{(t-t_0)^4}{4!} \left( g^2 \cos \theta_0 \sin \theta_0 + g \omega_0^2 \sin \theta_0 \right) \; .\]

Unlike the Kepler case, the resulting Lie series for the pendulum doesn’t neatly separate into two pieces linear in the initial conditions. In addition, it isn’t at all clear how this expansion relates to the classical solution in terms of elliptic integrals. So it seems that in spite of its universal applicability, the Lie series is not a silver bullet.

Next week, I’ll take a look how closely the two approaches match numerically.