For this go around with the Lie series, I thought it would be interesting to experiment with a problem quite unfamiliar to me – namely the full nonlinear pendulum equation. The approach here is two-fold. First, the classical computation for this key problem is presented. For this part, I use Lowenstein’s discussion in the book ‘Essentials of Hamiltonian Dynamics’ as a model. In the second part, I apply the Lie series to the system to see how well the generated expansion matches the classical result. The classical result requires a lot of familiarity with special functions and some clever and unmotivated substitutions. The hope here is that the brute force and straightforward method provided by the Lie series will be accurate enough when compared with the classical result to make it attractive.

Now to set the notation and conventions, consider the following figure of the pendulum.

The angle $$\theta$$ from the vertical is clearly the only relevant degree of freedom. The pendulum bob of mass $$m$$ possesses a kinetic energy of

\[ K = \frac{1}{2} m R^2 \dot \theta^2 \; ,\]

where $$R$$ is the length of the pendulum. As denoted in the figure, the zero of the potential energy is taken when the bob is horizontal so that $$\theta = \frac{\pi}{2}$$. The potential energy function is then

\[ U = – m g R \cos \theta \; ,\]

For convenience in what follows, set $$m = 1$$ and $$R = 1$$. The Lagrangian of the system is then

\[ L(\theta,\dot \theta) = \frac{1}{2} \dot \theta ^2 + g \cos \theta \]

with the corresponding Euler-Lagrange equations of

\[ \ddot \theta + g \sin \theta = 0 \; .\]

The conjugate momentum

\[ p_{\theta} = \frac{\partial L}{\partial \dot \theta} = \dot \theta \]

becomes the new independent variable in the system when we switch to the Hamiltonian

\[ H(\theta,p_{\theta}) = \frac{p_{\theta}^2}{2} – g \cos \theta \; .\]

Since $$H(\theta,p_{\theta})$$ has no explicit time dependence,

\[ \frac{d H}{dt} = \frac{\partial H}{\partial t} = 0 \; ,\]

it is a conserved quantity that is the total energy.

With the conservation firmly in hand, we can eliminate the conjugate momentum in favor of the generalized velocity to get the energy equation

\[ \frac{1}{2} \dot \theta ^2 – g \cos \theta = E \; .\]

At this point, the special function gymnastics begin with the substitutions

\[ z = \frac{1}{k} sin \left( \frac{\theta}{2} \right) \]
and
\[ k = \sqrt{ \frac{E + g}{2 g} } \; ,\]

which bring the energy equation into the form

\[ \dot z ^2 = g(1-k^2 z^2) (1 – z^2) \; .\]

Solving this for $$dt$$ gives

\[ dt = \frac{dz}{ \sqrt{ g(1-k^2 z^2) (1 – z^2) } } \]

which integrates to

\[t – t_0 = \frac{1}{\sqrt{g}} \int_0^z \frac{d \zeta}{\sqrt{ g(1-k^2 \zeta^2) (1 – \zeta^2)}} \]

The integral on the right-hand side is important enough to have its own name – it is an elliptic integral of the first kind and its solutions are defined as

\[ F(sin^{-1} z|k^2) \equiv \frac{1}{\sqrt{g}} \int_0^z \frac{d \zeta}{\sqrt{ g(1-k^2 \zeta^2) (1 – \zeta^2) }}\]

By construction, $$k^2 \in [0,1)$$ corresponds to the librating situation where the bob has only enough energy to move to and fro without spinning about it point of rotation. The classical solution for $$z$$ is compactly written as

\[ z = sn(\sqrt{g}(t-t_0),k^2) \]

where $$sn$$ is the Jacobi elliptic integral. Inverting the defining relation between $$z$$ and $$\theta$$ gives the final solution as

\[ \theta(t) = 2 \sin^{-1}\left(k sn(\sqrt{g}t,k^2) \right) \; .\]

Understanding how to mine information from these expressions requires a fairly sophisticated understanding of the elliptical integrals, which, while important for this key problem, don’t translate universally.

To apply the Lie series, rewrite the equations of motion in state space form

\[ \frac{d}{dt} \left[ \begin{array}{c} \theta \\ \omega \end{array} \right] = \left[ \begin{array}{c} \omega \\ – g \sin \theta \end{array} \right] \]

from which is read the differential operator

\[ D = \omega_0 \partial_{\theta_0} – g \sin \theta_0 \partial_{\omega_0} \; .\]

The solution to the problem is then given by
\[ L[\theta_0] = e^{(t-t_0)D} \theta_0 \; .\]

As is usually the case, the Lie series is tractable to hand computations for the first few terms. The relevant operations with $$D$$ are:

\[ D \theta_0 = \omega_0 \; ,\]

\[ D^2 \theta_0 = – g \sin \theta_0 \; , \]

\[ D^3 \theta_0 = – g \omega_0 \cos \theta_0 \; , \]

and

\[ D^4 \theta_0 = g^2 \cos \theta_0 \sin \theta_0 + g \omega_0^2 \sin \theta_0 \; .\]

The resulting Lie series is quite unwieldy resulting in

\[ L[\theta_0] = \theta_0 – g \frac{(t-t_0)^2}{2!} \sin \theta_0 + \left( (t-t_0) – g \frac{(t-t_0)^3}{3!} \cos \theta_0 \right) \omega_0 \\ + \frac{(t-t_0)^4}{4!} \left( g^2 \cos \theta_0 \sin \theta_0 + g \omega_0^2 \sin \theta_0 \right) \; .\]

Unlike the Kepler case, the resulting Lie series for the pendulum doesn’t neatly separate into two pieces linear in the initial conditions. In addition, it isn’t at all clear how this expansion relates to the classical solution in terms of elliptic integrals. So it seems that in spite of its universal applicability, the Lie series is not a silver bullet.

Next week, I’ll take a look how closely the two approaches match numerically.

This week the Lie series faces a stiff challenge in the form of the Kepler problem. Unlike some of the cases previously examined in this blog (harmonic oscillator, quantum wave propagation, etc.) the Kepler problem is nonlinear when written in the usual fashion in terms of Cartesian coordinates. There is a standard ‘clever’ substitution that make everything look linear ($$u = 1/r$$) but this won’t be employed.

In terms of the Cartesian coordinates, the orbital state for the Kepler problem is

\[ \bar s = \left[ \begin{array}{c} \vec r \\ \vec v \end{array} \right] \; ,\]

where $$\vec r$$ and $$\vec v$$ are the position and velocity of a reduced mass moving in a central potential $$V(r) = 1/r$$.

The equations of motion in state space notation are

\[ \frac{d}{dt} \bar S = \left[ \begin{array}{c} \vec v \\ -\frac{\mu \vec r}{r^3} \end{array} \right] \; ,\]

with initial conditions $$\vec r(t_0) = \vec \rho$$ and $$\vec v(t_0) = \vec \nu$$.

The corresponding Lie operator, which is written in terms of the initial conditions is

\[ D = \sum_i \nu_i \frac{\partial}{\partial \rho_i} – \frac{\mu \rho_i} {\rho^3} \frac{\partial}{\partial \nu_i } \; \]

or more compactly (with some slight abuse of notation)

\[ D = \vec \nu \cdot \partial_{\vec \rho} – \epsilon \vec \rho \cdot \partial_{\vec \nu} \; ,\]

where $$\epsilon = \mu/\rho^3$$ has been defined for future convenience.

The full solution is then given by the application of the Lie series operator $$L$$ to the initial position $$\vec \rho$$

\[ \vec r(t) = L[ \vec \rho ] \; .\]

With $$D$$ being nonlinear, the expansion implicit in this solution is very difficult to evaluate to all orders so a truncation of the expansion to order $$(t-t_0)^3$$

\[ L[\vec \rho] = e^{(t-t_0) D} \vec \rho \approx \left[ 1 + (t-t_0) D + \frac{ (t-t_0)^2}{2!} D^2 + \frac{(t-t_0)^3}{3!} D^3 \right] \vec \rho \]

will be employed with an eye for what patterns emerge.

A little bit of organization usually serves well in these types of expansions and, with that in mind, we note the following evaluations

\[ D \vec \rho = \vec \nu \; ,\]

\[ D^2 \vec \rho = D \vec \nu = – \frac{ \mu }{\rho^3} \vec \rho = – \epsilon \vec \rho \; ,\]

and

\[ D^3 \vec \rho = D( -\epsilon \vec \rho) = -\vec \nu \cdot \partial_{\vec \rho} \epsilon – \epsilon \vec \nu \; . \]

The third order expansion takes the form

\[ L[\vec \rho] \approx \vec \rho + (t-t_0) \vec \nu – \frac{ (t-t_0)^2 }{2!} \epsilon \vec \rho – \frac{ (t-t_0)^3 }{3!} \left( \vec \nu \cdot \partial_{\vec \rho} \epsilon + \epsilon \vec \nu \right) \; .\]

The last remaining partial derivative evaluates to

\[ \vec \nu \cdot \partial_{\vec \rho} \epsilon = \vec \nu \cdot \partial_{\vec \rho} \frac{\mu}{\rho^3} = -\frac{3 \vec \nu \cdot \vec \rho \mu}{\rho^5} \; . \]

Defining one last ‘greek’ shorthand (the reason for this will emerge shortly)

\[ \lambda = \frac{\vec \nu \cdot \vec \rho}{\rho^2} \]

allows the expansion to take the form

\[ L[\rho] \approx \vec \rho + (t-t_0) \vec \nu – \frac{ (t-t_0)^2 }{2!} \epsilon \vec \rho – \frac{ (t-t_0)^3 }{3!} \left( 3 \epsilon \lambda \vec \rho – \epsilon \vec \nu \right) \; .\]

What to make of this expansion? Compare this against the Taylor’s series expansion of the position (see ‘An Introduction to the Mathematics and Methods of Astrodynamics, Revised Edition’ by Battin, pp 110-112)

\[ \vec r(t) = \vec r0 + (t-t0) \left . \frac{d \vec r}{dt} \right|_{t=t0} + \frac{(t-t0)^2}{2!} \left. \frac{d^2 \vec r}{d t^2} \right|_{t=t0} \\ + \frac{(t-t0)^3}{3!} \left. \frac{d^3 \vec r}{d t^3} \right|_{t=t0} + \cdots \; .\]

Apparently, Lagrange defined the following ‘invariants’ (there are three of them but I’m only using the first 2)

\[ \epsilon = \frac{\mu}{r^3} \]

and

\[ \lambda = \frac{ \vec r \cdot \vec v }{ r^2 } \; \]

In terms of these classical invariants, the first three derivatives in the Taylors series become

\[ \frac{d \vec r}{dt} = \vec v \; , \]

\[ \frac{d^2 \vec r}{dt^2} = -\epsilon \vec r \; ,\]

and

\[ \frac{d^3 \vec r}{dt^3} = 3 \epsilon \lambda \vec r – \epsilon \vec v \; .\]

The series expansion thus agrees with the Lie series method or, in other words, the Lie series has reproduced the classical Lagrange f-g series

\[ \vec r(t) = f(t) \vec \rho + g(t) \vec \nu \; .\]

While there is really no new content that the Lie series has provided it does provide a few advantages. The first is that the notation is much more compact than the traditional approach using the Lagrange invariants. Second, the Lie series is clearly extensible to other, more complex problems and in such a fashion that is seems to provide a theoretical insight.

I’ll try to flesh this idea out next week when I apply the Lie series to the pendulum problem.

This column, which is a relatively short one as I am still grappling with the details, is the introductory piece for what I intend to be a through exploration of the use of Lie Series as a method for solving differential equations. This particular entry is heavily influenced by the NASA Technical Note TN D-4460 entitled ‘On the Application of Lie-Series to the Problems of Celestial Mechanics’ by Karl Stumpff, dated June 1968.

Stumpff starts his note with the following interesting passage:

That passage is interesting mostly due what the meaning of ‘Recently’ is. In his references, Stumpff lists only one work by Grobner, entitled “Die Lie-Reihen und ihre Anwendungen” dated 1960. Sophus Lie, from whom the Lie series derives it’s name, died in 1899 and it seems that it took 61 years for his work to really penetrate celestial mechanics.

The central idea of the Lie series is the production of an operator that makes the solution of certain differential equations manifest and their expansion in terms of a power series ‘automatic’. In presenting the prescription, I follow Stumpff’s ordering closely but with modifications of the notation to suit my tastes and needs.

Assume that there are $$n$$ functions

\[ F_i(z) = F_i(z_1, z_2, \dots, z_n) \]

in $$n$$ complex variables $$z_i$$ that are analytic in the neighborhood of

\[ \zeta = (\zeta_1, \zeta_2, \dots, \zeta_n) \; . \]

The concept of a Lie series depends on first defining the operator

\[ D = F_1(z) \frac{\partial}{\partial z_1} + F_2(z) \frac{\partial}{\partial z_2} + \dots + F_n(z) \frac{\partial}{\partial z_n} \; .\]

The operator $$D$$ is a derivation. That is to say it obeys the following properties.

It is linear

\[ D[f(z) + g(z) ] = D[f(z)] + D[g(z)] \; ,\]

it operation on a constant results in zero

\[ D[ c f(z) ] = c D f(z) \; , \]

and it obeys the Liebniz rule

\[ D[f(z) g(z) ] = f(z) \cdot Dg(z) + Df(z) \cdot g(z) \; .\]

Repeated application of the $$D$$ operator on the product of two functions results in the usual binomial expansion

\[ D^n [ f(z) g(z) ] = \sum_{\nu = 0}^{n} \left( \begin{array}{c} n \\ \nu \end{array} \right) D^{\nu} f(z) D^{n-\nu} g(z) \; .\]

Now the Lie series operator $$L$$ is defined as

\[ L(z,t) f(z) = e^{t D} f(z) \; , \]

where the exponential notation is short-hand for the series

\[ L(z,t) f(z) = \sum_{n=0}^{\infty} \frac{t^n}{n!} D^n f(z) = \left[1 + t D + \frac{t^2}{2!} D^2 + \dots \right] f(z) \; .\]

Note that often, the arguments $$(z,t)$$ are omitted.

Now an interesting and useful property of the Lie series operator for the product of two functions is

\[ L[f(z)g(z)] = L[f(z)] \cdot L[g(z)] \; ,\]

or in words, that the Lie series of a product is the product of the Lie series. This relationship is called the interchange relation.

Since we imagine that all the functions of interest are analytic, this simple relation ‘bootstraps’ to the general relation

\[ L[ Q(z)] = Q(L[z]) \; ,\]

for $$Q(z)$$ analytic.

As an example of this bootstrap relation, consider $$D = \frac{d}{dz}$$, and note that

\[ D^n[z] = 1 \delta_{n0} \]

and therefore

\[ L[z] = e^{t D}z = (1+ tD)z = z + t \; .\]

So the bootstrap relation gives first

\[ L[ Q(z)] = \sum_{n=0}^{\infty} \frac{t^n}{n!} \frac{d}{dz} Q(z) \; ,\]

which from elementary calculus is recognized to be $$Q(z+t)$$ expanded about $$t=0$$, and second

\[ Q(L[z]) = Q(z+t) \; . \]

Now the utility of the Lie series is not that it provides a compact way of representing a Taylor’s series (as convenient as that is) but rather in the fact that when the $$F_i$$ are not trivial functions it encodes solutions to a coupled set of differential equations. To see how this works, assume a system of differential equations given by

\[ \frac{d z_i}{dt} = F_i(z) \]

with initial conditions

\[ z_i(0) = \zeta_i \; .\]

Then the solution of this system of equations is

\[ z_i(t) = e^{t D} \zeta_i \; . \]

To see this, take the derivative of the solution to get

\[ \frac{d z_i(t)}{d t} = \frac{d}{dt} e^{tD} \zeta_i = D e^{t D} \zeta_i \; . \]

But, by definition, $$ e^{t D} \zeta_i = z_i(t) $$, so

\[ \frac{d z_i(t)}{d t} = D z_i = F_i \; . \]

In some sense, this is our old friend the propagator or state transition matrix written in a new form. However, this new encoding works for non-linear systems as well, a point that makes it an improvement on those approaches.

One last note. So far, the system of differential equations was assumed to be autonomous. In the event the system isn’t, a simple ‘trick’ can be used to make it look autonomous. Define a new variable $$z_0 = t$$ and the augment the definition of $$D$$ to be

\[ D = \frac{\partial}{\partial z_0} + \sum_{i=0}^{n} F_i(z) \frac{\partial}{\partial z_i} \; .\]

This manipulation has the advantage of making an non-autonomous system look formally autonomous. The only disadvantage is that all notion of equilibrium points are lost since the right-hand side of the equations can never have well-defined critical points.

Next time, I’ll apply the Lie series formalism to the Kepler problem

Last week, we discussed how a clever interrogation of the Maxwell’s equations to find a variety of relations, including the derivation of Poynting’s theorem. This week, I thought it would be interesting to look a little more at how the Poynting’s theorem works for a set of special cases.

The first case looks at the propagation of the an electromagnetic wave. In this case, common intuition as to the direction of the energy flow will match the mathematics and all looks right with the world. The second case involves a uniform current is put through a resistive wire. This common situation ends up an unusual interpretation of the Poynting flux. The third case, which involves running AC current through a capacitor in a circuit, common intuition about the direction of $$\vec S$$ turns out to be quite wrong and the result is both puzzling and instructive.

On note, before the dissection of the two cases begins. This post is heavily influenced by Chapter 10 in Electromagnetic Theory by Frankl and the discussion in Chapter 27 of the Feynman Lectures on Physics.

Case 1 – Propagation of an Electromagnetic Wave

One of the most celebrated results of Maxwell’s synthesis of the equations that bear his name and which follows from and, in some sense, motivated his inclusion of the displacement term in Ampere’s law is the prediction of electromagnetic waves. From the basic equations, a plane electromagnetic wave of frequency $$\omega$$ propagating in the $$k$$-direction (which can point anywhere) is described by

\[ \vec E(z,t) = \vec E_0 e^{i(\vec k \cdot \vec r – \omega t)} \]

for the electric field and by

\[ \vec B(z,t) = \vec B_0 e^{i(\vec k \cdot \vec r – \omega t)} \]

for the magnetic field.

Note that this form assumes that the wave propagates in free space and, therefore, doesn’t interact with matter. Applying Coulomb’s law ($$div(\vec E) = 0$$) gives

\[ \nabla \cdot \vec E = 0 \Rightarrow \vec E_0 \cdot \vec k = 0 \; .\]

Likewise, the application of the Monopole law leads to $$\vec B_0 \cdot \vec k = 0$$. So the electric and magnetic fields are perpendicular to the direction of propagation and since $$\vec S = \vec E \times \vec B / \mu_0$$ the Poynting flux is parallel to $$\vec k$$ just as common intuition indicates. The energy flow is along the direction of propagation.

Note that a careful computation will show that the magnitude of the energy flow is just what elementary wave mechanics would predict.

Case 2 – Current Through a Resistive Wire

In this case, a long straight wire with conductivity $$g$$ carries a current $$I$$ uniformly distributed across it. The relevant geometry is shown in the figure.

The current density is

\[ \vec J = \frac{I}{\pi a^2} \hat z \; .\]

The electric field needed to drive this current is

\[ \vec E = I R \hat z = I \frac{1}{\pi a^2 g} \hat z \]

and the resulting magnetic field set up by the current (by applying Ampere’s law) is

\[\vec H = \left\{ \begin{array}{c} \frac{I \rho}{2 \pi a^2 } \hat \phi \; \; \text{for} \; \; \rho < a \\ \frac{I}{2 \pi \rho} \hat \phi \; \; \text{for} \; \; \rho >a \end{array} \right. \; , \]

where $$\hat \phi$$ is the unit vector pointing along the azimuthal angle direction and $$\hat \rho$$ points along the radial direction in cylindrical coordinates (i.e. both are confined to the $$x$$-$$y$$ plane in cylindrical coordinates). The Poynting vector evaluates to

\[\vec S = \left\{ \begin{array}{c} -\frac{I^2 R}{2 \pi} \frac{\rho}{a^2} \hat \rho \; \; \text{for} \; \; \rho < a \\ - \frac{I^2 R}{2 \pi} \frac{1}{\rho} \hat \rho \; \; \text{for} \; \; \rho > a \end{array} \right. \; .\]

Note the peculiar nature of the direction of the energy flow. It isn’t along the wire but radially in from the outside.

Now a concern may be raised that there is an error somewhere hidden in the manipulations up to date. To assuage these concerns and build confidence, compute the divergence of the Poynting vector. The result should be related to the energy dissipation happening due to the resistance. The divergence is (recall that, in cylindrical coordinates, $$\nabla \cdot (A_{\rho} \hat \rho) = \frac{1}{\rho} \partial_{\rho} (\rho A_{\rho})$$) :

\[\nabla \cdot \vec S = \left\{ \begin{array}{c} -\frac{I^2 R}{\pi a^2} \; \; \text{for} \; \; \rho < a \\ 0 \; \; \text{for} \; \; \rho > a\end{array} \right. \; . \]

The dissipation within the wire is given by

\[ \vec E \cdot \vec J = \frac{I^2 R}{\pi a^2} \; ,\]

and the Poynting theorem is

\[ \nabla \cdot \vec S + \partial_t u = – \vec E \cdot \vec J \; .\]

Since the situation is static, all partial time derivatives are zero and we should see that $$\nabla \cdot \vec S = – \vec E \cdot \vec J$$, which happily is the result. So, despite what may seem to fly in the face of intuition, the theory holds together.

Case 3 – Run AC Current Through a Capacitor

This case is an intermediate case between the previous two, in which a low-frequency current is driven through a capacitor. This situation is intermediate between the first two – it does not involve static fields but does confine the action to a local circuit element. The relevant geometry is shown in the following figure.

Assuming that the frequency is small enough to ignore the energy in the magnetic field, the total energy contained between the plates is

\[ U_{tot} = u \cdot Vol = (\frac{1}{2} \epsilon_0 E^2)(\pi a^2 h) \]

and it changes as function of time as

\[ \partial_t U_{tot} = \epsilon_0 \pi a^2 h E \partial_t E \; .\]

From an application of Ampere’s law applied to the surfaces of the capacitor, converting the surface integral over $$curl(\vec B)$$ to a line integral along the boundary and using $$\mu_0 \epsilon_0 = 1/c^2$$, yields

\[ 2 \pi a c^2 B = \partial_t E \pi a^2 \; ,\]

which solved for $B$ gives

\[ B = \frac{a}{2 c^2} \partial_t E \; .\]

The direction of $$\vec E$$ is along the axial direction of the capacitor and the direction of $$\vec B$$ is azimuthal. From these facts, it is obvious that the Poynting vector must be pointing radially inward, as shown in the figure.

The magnitude of the Poynting vector is (note the simplification since the electric and magnetic field are perpendicular)

\[ |\vec S| = |\vec E| |\vec B| =\frac{1}{\mu_0} E \frac{a}{2 c^2} \partial_t E = \frac{1}{2} \epsilon_0 a E \partial_t E \; . \]

The total energy flow in is given by the product of the magnitude of the Poynting vector times the total surface area

\[ \Delta U = |\vec S| \cdot Area = (\frac{1}{2} \epsilon_0 a E \partial_t E) (2 \pi a h) = \epsilon_0 \pi a^2 h E \partial_t E \; , \]

which is happily the same result we got above.

So once again, the flow of the energy seems counterintuitive but the results that follow agree with what is expected.

One of the more fun things to do with physical models is to mine general results without actually solving specific problems. Its fun because it is relatively easy to do and gives some global insight into the problem that is not easily obtainable from examining individual cases. Usually, this type of data mining comes from considerations of symmetry or general principles and takes the form of clever manipulations of the underlying equations. Like any good riddle, the joy is in seeing the solution – the frustration is in trying to find it for the first time.

Of course, to find these nuggets of general fact, one needs to know, or at least firmly believe, they are there. Conservation laws for energy, momentum, and angular momentum are cherished principles that took many decades to be ferreted out of many specific cases.

Nonetheless, we can all stand on the shoulders of giants and enjoy the view and that is what this post is all about. Standing on the shoulders of Maxwell, one can mine the equations that bear his name for all sorts of nuggets.

The version of Maxwell’s equations that I’ll use describes the behavior of the macroscopic fields with the appropriate constitutive equations. These are:
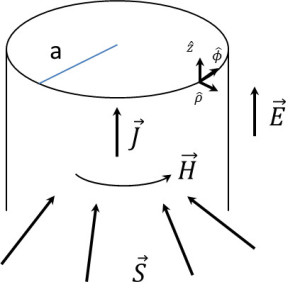
\[ \nabla \times \vec H = \vec J + \frac{\partial \vec D}{\partial t} \; , \]
\[ \nabla \times \vec E = -\frac{\partial \vec B}{\partial t} \; ,\]
\[ \nabla \cdot \vec D = \rho \; ,\]
and
\[ \nabla \cdot \vec B = 0 \; , \]
as the differential expressions for Ampere’s, Faraday’s, Coulomb’s and the Monopole’s laws.

Since dimensional analysis will be important below, note that fields and sources have units of

• $$\vec E$$ – $$[N/C]$$ or $$[V/m]$$
• $$\vec D$$ – $$[C/m^2]$$
• $$\vec B$$ – $$[Ns/Cm]$$ or $$[kg/Cs]$$
• $$\vec H$$ – $$[A/m]$$
• $$\vec J$$ – $$[C/m^2/s]$$
• $$\rho$$ – $$[C/m^3]$$
• $$\epsilon$$ – $$[C^2/Nm]$$
• $$\mu$$ – $$[N/A^2]$$

There are three very nice interrogations of these laws that yield: 1) charge conservation, 2) energy and momentum conservation (in the absence of external forces), and 3) the guarantee that a solution to the initial value problem (Coulomb and monopole equations) is preserved by the propagation of the system forward in time. This latter property will be called constraint preservation.

Charge Conservation

As they appear in their usual form, the Maxwell equations don’t immediately show that they honor the conservation of charge. That they actually do is seen by first starting with Ampere’s law and take the divergence of both sides to get

\[ \nabla \cdot \left( \nabla \times \vec H = \vec J + \frac{\partial \vec D}{\partial t} \right ) \Rightarrow \nabla \cdot \nabla \times \vec H = \nabla \cdot \vec J + \nabla \cdot \frac{\partial \vec D}{\partial t} \; . \]

Since the divergence of a curl is zero, the left-hand side disappears. Next interchange of the divergence operator with the partial derivative with respect to time, $$\partial_t$$ to get

\[ 0 = \nabla \cdot \vec J + \frac{\partial ( \nabla \cdot \vec D )}{\partial t} \; . \]

Now the last term on the right-hand side can be put into familiar form by using Coulomb’s law and, with one more minor manipulation, yields the familiar form of the charge conservation law

\[ \nabla \cdot \vec J + \frac{\partial \rho}{\partial t} = 0 \; .\]

Energy and Momentum Conservation

The starting point for this conservation is the proof of the Poynting theorem. Form the dot product between $$\vec H$$ and both sides of Faraday’s law to get

\[ \vec H \cdot \nabla \times \vec E = – \vec H \cdot \partial_t \vec B \]

Rewrite the left-hand side using the vector identity

\[ \nabla \cdot (\vec A \times \vec B) = (\nabla \times \vec A) \cdot \vec B – \vec A \cdot (\nabla \times \vec B) \]

giving

\[ \nabla( \vec E \times \vec H ) + \vec E \times (\nabla \times \vec H) = – \vec H \cdot \partial_t \vec B \]

Now use Ampere’s law to substitute for $$\nabla \times H $$, yielding

\[ \nabla( \vec E \times \vec H ) + \vec E \times (\vec J + \partial_t \vec D) = – \vec H \cdot \partial_t \vec B \]

which, when rearranged, gives the Poynting theorem

\[ \nabla \cdot (\vec E \times \vec H ) + \vec H \cdot \partial_t \vec B + \vec E \cdot \partial_t \vec D = – \vec E \cdot \vec J \]

Make the following identifications

\[ \vec S = \vec E \times \vec H \]

and

\[ u = \frac{1}{2} \left( \vec E \cdot \vec D + \vec H \cdot \vec B \right) \]

to get the common form of

\[ \nabla \cdot \vec S + \partial_t u = – \vec E \cdot \vec J \]

for Poynting’s theorem.

Now for some dimensional analysis. The quantities $$u$$, $$\vec S$$, $$\vec E \cdot \vec J$$, $$\nabla \cdot \vec S$$, and $$\partial_t u$$ have units of:

• $$u$$ – $$[N/C][C/m^2] + [Ns/Cm][C/sm]=[N/m^2] = [J/m^3]$$
• $$\vec S$$ – $$[N/C][C/sm] = [N/ms] = [Nm/m^2s] = [J/m^2s]$$
• $$\vec E \cdot \vec J$$ – $$[N/C][C/m^2s]=[Nm/m^3s] = [J/m^3s]$$
• $$\nabla \cdot \vec S $$ – $$[N/m^2s] = [Nm/m^3s] = [J/m^3s]$$
• $$\partial_t u$$ – $$[J/m^3][1/s] = [J/m^3s]$$

The obvious interpretation is that $$u$$ is an energy density, $$\vec S$$ is the energy flow (flux) and the $$\vec E \cdot \vec J$$ is the work done on the charges by the electric field per unit volume (power density).

There is a way to connect the Poynting theorem to momentum since photons obey $$E^2 = c^2 \vec p^2$$. For simplicity, the expression of the Poynting vector in free space and in terms of the magnetic permeability $$\mu_0$$ and the magnetic flux density $$\vec B$$ is

\[ \vec S = \frac{1}{\mu_0} \vec E \times \vec B \; .\]

A check of the Poynting vector units from the definition to find $$\underbrace{ [A^2/N] }_{1/\mu_0} \underbrace{ [N/C] }_{\vec E} \underbrace{ [Ns/Cm] }_{\vec B} = [N/ms]$$. Now these unit can be put into a more suggestive form as either $$[N/ms] = [Nm/m^3][m/s] = [J/m^3][m/s]$$, which suggests interpreting the Poynting vector as a energy density times a speed or as $$[N/ms] = [Nm][1/m^2/s] = [J/m^2/s] = [J/s/m^2] = [W/m^2]$$, which represents a power flux.

So dividing by the speed of light, in the appropriate form, gives

\[ \frac{1}{c} \vec S = \sqrt{ \frac{\epsilon_0}{\mu_0} } \vec E \times \vec B = \sqrt{ \epsilon_0 \mu_0 } \vec E \times \vec H \]

which represents either a momentum flux or a momentum density times speed. Since $$\vec S/c$$ has units of momentum density times speed one may guess that $$\vec S/c^2$$ is the field momentum density. This is true even in the presence of matter allowing the general definition of

\[ \frac{1}{c^2} \vec S = \underbrace{ \mu \epsilon \vec E \times \vec H}_{\text{field momentum density}} \; .\]

Frankl, in his Electromagnetic Theory (pp. 203-4), presents a nice argument, based on the Lorentz force law, to relate the field momentum to the particle momentum to show that

\[ \vec F_{total} = \frac{d}{dt}\left[ \vec p_{particles} + \int d^3 r \, \mu \epsilon \vec E \times \vec H \right] \; .\]

To see this, start with the Lorentz force law ($$\vec F = q (\vec E + \vec v \times \vec B)$$) expressed in terms of particle and field densities using Ampere’s and Coloumb’s laws

\[ \vec f = \rho \vec E + \vec J \times \vec B = (\nabla \cdot \vec D) \vec E – \vec B \times (\nabla \times \vec H) – \partial_t \vec D \times \vec B \; .\]

Using the Faraday and Monopole laws gives

\[ 0 = – \vec D \times (\nabla \times \vec E) – \vec D \times \partial_t \vec B \]

and

\[ 0 = – \vec H \, \nabla \cdot \vec B \; .\]

Adding the above relations to the Lorentz force law relation gives

\[ \vec f = \epsilon ( \vec E \, \nabla \cdot \vec E – \vec E \times (\nabla \times \vec E) ) + \mu ( \vec H \, \nabla \cdot \vec H – \vec H \times ( \nabla \times \vec H ) ) – \mu \epsilon \, \partial_t ( \vec E \times \vec H ) \; .\]

Integrate over all space using the identity

\[ \int d^3r \, (\vec G \nabla \cdot \vec G – \vec G \times \nabla \times \vec G) = \int d^2S \left( \vec G (\vec G \cdot \hat n) – \frac{1}{2} G^2 \hat n \right) \]

that allows two of the volume integrals to become surface integrals resulting in

\[ \underbrace{ \frac{d}{dt} \vec p_{particles} }_{\vec F_{particles}} = I_{\vec E} + I_{\vec H} – \frac{d}{dt} \int d^3r \, \mu \epsilon \vec E \times \vec H \; .\]

Finally, Frankl attaches meaning to the surface integrals by first looking at the situation where the fields are static to pick out the total force as

\[ \frac{d}{dt} \vec p_{particles} = \underbrace{ I_{\vec E} + I_{\vec H} }_{\text{total force}} \; .\]

Since the instantaneous configuration of the fields and the particles cannot ‘know’ the future, $$I_{\vec E} + I_{\vec H}$$ must always be the total force. Bring the field piece over to the left hand side gives

\[ \frac{d}{dt} \vec p_{particles} + \frac{d}{dt} \int d^3r \, \mu \epsilon \vec E \times \vec H = \underbrace{ I_{\vec E} + I_{\vec H} }_{\text{total force}} \; , \]

which suggests the identification of the field momentum as

\[ \vec p_{field} = \int d^3r \, \mu \epsilon \vec E \times \vec H \; ,\]

which is exactly the interpretation obtained above for the Poynting vector divided by the speed of light squared.

Now if the system is defined in such a way to be closed so that the electric and magnetic fields are zero on the boundary, then momentum and energy cannot flow out of the system and thus are conserved. Energy and momentum do flow between the particles and the fields, with one component gaining or losing as the other loses or gains, but never does any of the energy or momentum vanish.

Constraint Preservation

The two Maxwell equations involving the curl operator are dynamical – that is to say that the spatial derivatives are tied to derivatives with respect to time. The two Maxwell equations involving the divergence operator involve no time derivatives. This latter two are interpreted as constraint equations that the field must satisfy at each time step. The operative question is if the fields satisfy these constraints at some initial time, if the subsequent propagation of the field forward in time, described by the dynamical equations, really honors the constraints. That is to say, that the constraints will continue to be satisfied. This is a very important point, as any theory that fails to keep the constraints satisfied is physically untenable. To check whether Maxwell’s equations do preserve these constraints, start by taking the divergence of Ampere’s equation as in the charge conservation case above

\[ \nabla \cdot \vec J + \partial_{t} (\nabla \cdot \vec D ) = 0 \; .\]

This time, instead of hunting for charge conservation, we are going to use charge conservation to eliminate $$div(\vec J)$$ in favor of $$\partial_t \rho$$ to get

\[ -\partial_t \rho + \partial_t (\nabla \cdot \vec D) = 0 \Rightarrow \partial_t (\nabla \cdot \vec D – \rho ) = 0 \; .\]

Note that a logical purist may object that this constraint and charge conservation are really not independent of each other and that this ‘proof’ is merely a tautology. This is actually true but is not a flaw. It simply means that charge conservation and the preservation of the Coulomb go hand-in-hand.

Likewise, taking the divergence of Faraday’s law gives

\[ \nabla \cdot (\nabla \times \vec E + \partial_t \vec B = 0 ) \; , \]

which because of the divergence of the curl is zero becomes

\[ \partial_t (\nabla \cdot \vec B = 0 ) = 0 \; ,\]

assuming that $$\partial_t$$ commutes with $$\nabla \cdot$$.

Thus, once both Coulomb’s Law and the Monopole Law are satisfied at at the initial conditions, they stay satisfied for all time.

Last week, the problem of the conveyor belt accumulating some material at a steady rate $$r$$ was examined. The motor driving the belt kept it moving at a constant velocity. The power expended by the motor was double the power needed to accelerate the material when it hits the belt. The natural question is, why is it exactly double.

This question provoked a lot of discussion in ‘The Physics Teacher’, starting with an article by Wu, which tried to give a straightforward answer to why the value is exactly $$2$$ and also where did the other half of the energy go. For the most part, the argument by Wu, while physically intuitive, is lacking in logical rigor.

The best argument was given by Marcelo Alonso who starts with the varying-mass form of Newton’s law

\[ m \dot {\vec v} + {\dot m} (\vec v – \vec u) = \vec F_{ext} \; . \]

In this equation, $$m$$ is the system mass, which, in the case of the conveyor problem, is the mass of the belt and the material on it at any given time. The vector $$\vec v$$ is the velocity of the system. The quantities $$\dot m = r$$ and $$\vec u$$ are the rate of change of the system mass (more on this later) and the velocity of the mass that either enters of leaves the system, respectively. Justification for this equation will be given below.

The power imparted by the external force $$\vec F_{ext}$$ is

\[ {\mathcal P} = \vec F_{ext} \cdot \vec v = m \, \dot {\vec v} \cdot \vec v + \dot m (\vec v \cdot \vec v – \vec u \cdot \vec v) \; .\]

For the conveyor belt problem, the material enters with a very small velocity $$\vec u$$ that is perpendicular to the system velocity $$\vec v$$ so the last term vanishes. Since the motor keeps $$\vec v$$ constant it can be moved into and out of any total time derivative. The motor power is now

\[ {\mathcal P} = \dot m (\vec v \cdot \vec v) = \frac{d}{dt} \left( m \, \vec v \cdot \vec v \right) = \frac{d}{dt} ( 2 KE ) \; .\]

Viewed in this light, the factor of two is not so much mysterious as accidental. It is a consequence of the special circumstances that $$\vec u \cdot \vec v $$ is zero and $$\dot {\vec v} = 0$$. If the material were introduced to the belt in some other fashion, for example, thrown horizontally on the belt, the ratio of the power provided to the time rate of change of the materials kinetic energy would have been different and its value wouldn’t attract special attention.

All told this is a mostly satisfactory explanation. The only problem is that the terse response Alonso provided in the form of a letter to the editor didn’t give enough details on the varying-mass form of Newton’s law was derived.

Surprisingly, these details are difficult to find in most textbooks. Modern presentations don’t seem to care too much about varying mass situations although they are important in many applications. Systems in motion that suffer a mass change are almost everywhere in modern life. Examples range from cars that consume gasoline as they move, to ice accumulation on or water evaporation from industrial surfaces, to rocket motion and jet propulsion.

So in the interest of completeness, I derive the varying-mass form of Newton’s equations here.

There are two cases to consider: the system mass increases as material is accreted and the system mass decreases as material is ejected. The specific mechanisms of accretion or ejection are not important for what follows.

I will start with the accreting case just before a bit of matter $$\delta m$$ is introduced into the system mass. The initial momentum of the system and lump is

\[ \vec p_i = m \vec v + \delta m \, \vec u \; .\]

Just after this small lump has combined with the system, the final momentum is

\[ \vec p_f = ( m + \delta m)(\vec v + \delta \vec v) \; .\]

The change in momentum is the difference between these two quantities

\[ \Delta \vec p = \vec p_f – \vec p_i = ( m + \delta m)(\vec v + \delta \vec v) – m \vec v – \delta m \, \vec u \; ,\]

which simplifies to

\[ \Delta \vec p = m \, \delta \vec v + \delta m \, \vec v – \delta m \, \vec u \; .\]

This change is momentum is caused by the impulse due to the external force $$\vec F_{ext}$$

\[ \Delta \vec p = \vec F_{ext} \, \delta t \]

acting over the short time $$\delta t$$.

Equating the terms gives

\[ m \, \delta \vec v + \delta m \, \vec v – \delta m \, \vec u = \vec F_{ext} \, \delta t \; , \]

which becomes

\[ m \frac{\delta \vec v}{\delta t} + \frac{\delta m}{\delta t} ( \vec v – \vec u) = \vec F_{ext} \]

when dividing by the small time $$\delta t$$. Before this equation is taken to the limit and derivatives materialize out of deltas, let’s look at the ejection case.

For ejected mass, the system starts with the momentum

\[ \vec p_i = m \vec v \; .\]

After the lump with mass $$\delta m$$ is ejected with velocity $$\vec u$$, the final momentum takes the form

\[ \vec p_f = ( m – \delta m)(\vec v + \delta \vec v) + \delta m \, \vec u \;. \]

Following the same process above, the analogous equation

\[ m \frac {\delta \vec v}{\delta t} – \frac{\delta m}{\delta t} ( \vec v – \vec u) = \vec F_{ext} \]

results.

The two equations look similar with only a small change in sign in front of the $$\frac{\delta m}{\delta t}$$ to hint at the physical difference of mass inflowing in the first and outflowing in the second.

Sign differences can always be problematic and more so when it comes to ‘in’ versus ‘out’. Confusion can easily insert itself in such cases. As an example where careful track of sign conventions is important, consider the presentation of mass-varying systems in Halliday and Resnick. They present the mass ejection case as a preliminary to a discussion of rocket propulsion but they arrive at an equation with the opposite sign from the one derived here. They get this difference by explicitly setting the sign of $$dm/dt$$ opposite to that of $$\delta m/\delta t$$.

A small change in one’s frame of mind and a careful attention to the difference between $$\delta m/\delta t$$ and $$dm/dt$$ is all that is needed to reconcile these differences. To go from the simple ratios of deltas to actual derivatives, note that by the initial construction $$\delta m$$ was a positive quantity, a small bit of matter. The time increment $$\delta t$$ is also positive. So the ratio of these two quantities is also positive. But the rate of change of the system mass $$m$$ can be either positive or negative. Despite the notational similarity between $$\delta m/\delta t$$ and $$dm/dt$$, the mass $$m$$ being addressed is not the same. The mass in the derivative expression is the system mass which can gain or lose mass and so $$dm$$ can be positive or negative.

For the accreted mass case, $$dm/dt = r > 0$$ and the appropriate limit is

\[ m \frac{d \vec v}{d t} + \frac{d m}{dt} ( \vec v – \vec u ) = \vec F_{ext} \; ,\]

or, with an eye towards combining the two cases,

\[ m \frac{d \vec v}{d t} + \left| \frac{d m}{dt} \right| ( \vec v – \vec u ) = \vec F_{ext} \; .\]

For the ejected mass case, $$dm/dt = r < 0$$ and the appropriate limit is \[ m \frac{d \vec v}{d t} + \left| \frac{d m}{dt} \right| ( \vec v - \vec u ) = \vec F_{ext} \; ,\] with the sign on the second term now changing due to the inclusion of the absolute value.

The conservation of energy, which is so innocently applied in elementary applications, can be actually quite complicated when the system in question has mass flowing into or out of it. One of the most popular textbook questions for provoking thought on this topic is the conveyor belt.

Two well-known texts, ‘Mechanics’ 3rd ed., by Symon and ‘Physics’ by Halliday and Resnick, cover the conveyor belt problem, although in slightly different ways. Both start from a common setup of a belt moving at a constant velocity $$\vec v$$ onto which mass is dropped at a rate $$r = \frac{d m}{d t}$$ from a hopper above. The motor powering the conveyor applies a varying force $$\vec F$$ so that the constant velocity is maintained as the material mass $$m(t)$$ grows. For completeness, the mass of the belt is assigned a value $$M$$. Since the problem is one-dimensional, the explicit vector notation will be dropped in what follows.

The derivation starts with the mechanical momentum of the belt, defined as
\[ p(t) = [m(t) + M] v \; .\]

The time-varying motor force needed to maintain the constant velocity has to match the change in the momentum and thus
\[ F(t) = \frac{dp}{dt} = \frac{dm(t)}{dt} v = rv \; .\]

The power supplied by the motor is

\[ {\mathcal P} = F(t) v = v^2 \frac{dm(t)}{dt} = v^2 r \; , \]

which can be manipulated into a more familiar form since both $$v$$ and $$M$$ are constant, to yield

\[ {\mathcal P} = \frac{d}{dt}\left( m v^2 \right) = \frac{d}{dt} \left[ (m+M) v^2 \right] = 2 \frac{d}{dt} \left[ KE_{sys} \right ] \; . \]

In words, the motor supplies power that is twice is large as the change in the kinetic energy of the system. Halliday and Resnick also derive this two-to-one relationship. Both texts then ask where the excess half of the power going?

Of course, these authors expect that the student would infer where the energy has gone. His argument would start with the notion that the law of conservation of energy is cherished and believed to be correct in all cases. If half the supplied energy is easily found in the form of kinetic energy of the belt plus material the rest must be ‘hidden’ in a less obvious place. This missing other half must have been converted into some other form. Continuing on in this vein, the student would then conclude that a force is needed to accelerate each bit of mass introduced onto the belt and that that force can only be due to friction between the belt and the material so introduced. Once friction is introduced, it is a short and easy step to conclude that the extra energy is converted into the internal energy of the belt or the material.

Since this is the obvious path for such a venerable problem, it is hard to believe that there is any controversy surrounding this conclusion. But as Mu-Shiang Wu points out in ‘Note on a Conveyor-belt problem’, The Physics Teacher (TPT) 23, 220 (1986), the student is often puzzled why the missing energy happens to be half of the supplied power. By his presentation in that article, Wu also implies that the student is not satisfied with the broad and general conclusion that missing half is dumped into heat, he also wants to see the explicit mechanism. Wu’s argument to explain this mechanism goes something like this.

Follow a bit of mass $$\delta m$$ as it falls from the hopper. Relative to an observer riding along the belt, this chunk is moving with velocity $$-v$$. Since this bit of mass must come to rest with respect to the belt over some period of time $$\delta t$$ there must a be a frictional force $$F_f$$ that arrests the mass’s leftward motion. Wu posits the form of this frictional force to be

\[ F_f = \mu N = \mu \delta m g \; ,\]

where $$\mu$$ is the coefficient of kinetic (or sliding) friction, and $$N$$ is the normal force supplied by the belt. This kinetic friction force results in a constant acceleration $$a = \mu g$$. Using the standard the kinematic relations for constant acceleration

\[ x_f = x_i + v_i \delta t + 1/2 a \delta t^2 \]

and

\[ v_f = v_i + a \delta t\]

and eliminating the time $$\delta t$$ it takes for the friction force to bring the chunk of mass to a stop (i.e. $$v_f = 0$$) leads to the total distance traveled as

\[ D = \frac{v^2}{2 a} \; .\]

The work done by the frictional force is then

\[ \delta W = F_f D = \frac{1}{2} \delta m v^2 \; , \]

and the power exerted is

\[ {\mathcal P_f} = \frac{\delta W}{\delta t} = \frac{1}{2} \frac{\delta m}{\delta t} v^2 = \frac{d}{dt} \left( \frac{1}{2} m v^2 \right) \; .\]

At this point, Wu stops with the statement

Overall, I am suspicious of Wu’s argument. It has the attractive feature of having a explicit mechanism for the force that brings the material to rest on the conveyor belt but the use of the co-moving frame is done using a bit of a cheat. To demonstrate the roots of my suspicion, let me modify Wu’s argument starting just after the use of the constant acceleration kinematic equations. The total displacement (not distance) traveled is

\[ D = (x_f – x_i) = -\frac{v^2}{2 a} \; .\]

The work done by the frictional force is then (note the sign)

\[ \delta W = \int_{x_i}^{x_f} F_f dx = F_f (x_f – x_0) = -\frac{1}{2} \delta m v^2 \; .\]

Thus the chunk of mass loses energy in this frame and the power loss is

\[ \frac{\delta W}{\delta t} = -\frac{1}{2} \frac{\delta m}{\delta t} v^2 \]

or (taking the limit in the usual casual physicist style)

\[ {\mathcal P_f} = – \frac{d}{dt} \left( \frac{1}{2} m v^2 \right) \; .\]

The power lost by the object is exactly one half of the total power supplied by the belt. This loss is assumed to go into heat so the energy balance is satisfied in a hand-waving way but there is this pesky problem associated with the two different frames. So I don’t think the puzzle is satisfied.

In the intervening years (1987-1990) after Wu’s initial article was published a number of other author’s published notes, critiques, and alternative ways of thinking about the conveyor belt problem. Judging by the different points-of-view expressed, the original unanswered question by Symon and Halliday and Resnick seems to have assumed a manifest truth that is not as obvious once one digs in as it is on the surface. Almost none of the arguments I’ve read in TPT have swayed me except for a letter by Marcel Alonso in response to Wu’s original article.

Next week I’ll cover Alonso’s argument and some details about variable mass systems.

One of the more confusing things when I was learning vector calculus \& classical field theory was the derivation of the flux transport theorem. The theorem relates the change in flux $$\Phi$$ due to a vector field $$\vec F$$ through a moving surface $${\mathcal S}$$ to certain integrals involving the time rate of change and the divergence of the field over the surface along with a contour integral around the surface’s boundary. Using the notation of ‘Introduction to Vector Analysis, 4th ed.’ by Davis and Snider, the flux transport theorem is given by:

\[ \frac{d \Phi}{d t} = \int_{\mathcal S} d \vec {\mathcal S} \cdot \left[ \frac{\partial \vec F}{\partial t} + (\nabla \cdot \vec F) \vec v \right] + \int_{\partial {\mathcal S}} d \vec \ell \cdot \vec F \times \vec v \; , \]

where $$d \vec {\mathcal S}$$ is the outward normal to a differential portion of surface area, $$\vec v$$ is the velocity at each point on the surface (recall it is moving), and $$d \vec \ell$$ is a differential line element along the boundary of the surface $$\partial {\mathcal S}$$.

Davis and Snider have some nice homework problems but I wanted an example where the surface changed size as well as moved in space. The example I concocted is one with a rectangular shaped surface whose four vertices are given by:
\[ \vec {\mathcal A} \doteq [t,-t,-1] \; ,\]
\[ \vec {\mathcal B} \doteq [t,t,-1] \; ,\]
\[ \vec {\mathcal C} \doteq [t,t,1] \; ,\]
and
\[ \vec {\mathcal B} \doteq [t,-t,1] \; .\]
Note that I represent ($$\doteq$$) the coordinates of the points by row arrays simply for typographical convenience, although whether they are rows or columns doesn’t matter.

The surface, which moves uniformly in the x-direction, is canted 45 degrees with respect to the y-z plane and has a time varying area of $$4t$$. The surface is parametrized by two parameters $$u$$ and $$v$$ ranging from $$0$$ to $$1$$ such that any point on the surface (including the boundary) is given by

\[\vec {\mathcal R}(u,v) \doteq \left[ t, (2u-1)t, 2v -1 \right] \; \; u,v \in[0,1] \; .\]

In this parameterization, the outward normal to a differential patch is

\[ d \vec {\mathcal S} = \frac{\partial \vec {\mathcal R}}{\partial u} \times \frac{\partial \vec {\mathcal R}}{\partial v} du dv \doteq [4t,0,0] du dv \; , \]

from which we immediately get the total area as

\[ Area(\vec {\mathcal S}) = \int_{(u,v)} |d \vec {\mathcal S} | = \int_0^1 du \int_0^1 dv \, 4 t = 4t \]

as expected.

The form of the vector field is

\[ \vec F(\vec r) \doteq [x y^2, y z^2 z x^2] \]

where $$\vec r \doteq [x,y,z] $$.

Since the form of the surface and the vector field are fairly simple, the flux through the surface due to $$\vec F$$

\[ \Phi[\vec F,\vec {\mathcal S}] = \int_{\vec {\mathcal S}} \vec F(\vec {\mathcal R}(u,v)) \cdot d \vec {\mathcal S} \]

can be explicitly computed as
\[ \Phi[\vec F,\vec {\mathcal S}] = \int_0^1 du \int_0^1 dv \, 4 t^4 (2 u – 1)^2 = \frac{4t^4}{3} \; .\]

The time derivative is then easily obtained as

\[ \frac{d \Phi[\vec F,\vec {\mathcal S}]}{d t} = \frac{16t^3}{3} \; .\]

To use the flux transport theorem, we need to compute $$div(\vec F)$$ and $$\frac{\partial \vec F}{\partial t}$$ and then evaluate these terms across the expanse of the surface $$\mathcal{S}$$. Likewise we also need to compute $$\vec F \times \vec v$$, where $$\vec v$$ is the velocity of the surface and then evaluate this terms along the its boundary.

The divergence of the field is given by

\[ div(\vec F) = x^2 + y^2 + z^2 \; , \]

which, in the $$u-v$$ parametrization becomes

\[ div(\vec F) = t^2 + (2 u – 1)^2 t^2 + (2 v- 1)^2 \; .\]

The time derivative of the field is

\[\frac{\partial \vec F}{\partial t} = 0 \]

since the vector field $$\vec F$$ has no explicit time dependence. All of the time rate of change is due to the surface moving within the field.

The surface integral in the flux transport equation, formally given by

\[ I_0 = \int_{\vec {\mathcal S}} d \vec {\mathcal S} \cdot \left[ div\left(\vec F(\vec {\mathcal R}(u,v))\right) \vec v + \frac{\partial \vec F}{\partial t}\left(\vec {\mathcal R}(u,v)\right) \right] \]

in the $$u-v$$ parametrization, evaluates to

\[ I_0 = \frac{ 16 t^3}{3} + \frac{4 t }{3} \; .\]

The velocity of any point on the surface is obtained by taking a time derivative with respect to $$\vec {\mathcal R}$$

\[ \vec v = \frac{\partial \mathcal{R} (u,v)}{\partial t} \doteq [1, 2 u – 1, 0] \; .\]

The integrand of the line integral is

\[ \vec F \times \vec v \doteq [ – z x^2 (2 u – 1), z x^2 , x y^2 (2 u – 1) – y z^2 ] \; , \]

which, in the $$u-v$$ parametrization, becomes

\[ \vec F \times \vec v \doteq [-(2 v – 1)(2 u – 1) t^2, (2 v – 1) t^2, (2 u – 1)^3 t^3 – (2 u – 1)(2 v – 1 )^2 t] \; .\]

There are four distinct lines or legs making up the boundary of the surface. These are given by

\[ \vec {\mathcal L}_1(u) = \vec {\mathcal A} + u(\vec {\mathcal B} – \vec {\mathcal A}) \; ,\]
\[ \vec {\mathcal L}_2(v) = \vec {\mathcal B} + v(\vec {\mathcal C} – \vec {\mathcal B}) \; ,\]
\[ \vec {\mathcal L}_3(u) = \vec {\mathcal C} + u(\vec {\mathcal D} – \vec {\mathcal C}) \; ,\]

and

\[ \vec {\mathcal L}_4(v) = \vec {\mathcal D} + v(\vec {\mathcal A} – \vec {\mathcal D}) \]

and there is a corresponding integral for each.

The evaluation of each is a bit tedious (particularly in taking care to make sure that $$u$$ or $$v$$ take on the appropriate value for the leg being traversed) but straightforward leading to
\[ I_1 =-2 t^3 \int_0^1 du = -2 t^3 \; , \]
\[ I_2 = 2 t^3 \int_0^1 dv – 2t \int_0^1 dv (2v-1)^2 = \frac{ 2(3 t^3 – t)}{3} \; , \]
\[ I_3 = -2t^3 \int_0^1 du = -2 t^3 \; , \]
and

\[ I_4 = 2 t^3 \int_0^1 dv – 2t\int_0^1 dv (2v-1)^2 = 2 t^3 – \frac{2}{3} t \; ,\]
respectively.

The total line integral around the boundary is then given as the sum of these terms

\[ I_c = – \frac{4}{3} t \; .\]

Adding this result to the result from surface integral gives

\[I_{tot} = \frac{16 t^3}{3} \; , \]

which is the same result as before.

While this example is a bit contrived, it does offer a simple combination of both movement and growth that seems absent within the literature. Furthermore, when worked in detail, each piece drives home the content of the flux transport theorem.

This week I’ve decided to take a look at an innocent-looking experiment from elementary mechanics that is a lot more subtle than I think most people realize. I justify this assertion from the many incorrect statements concerning this experiment that can be found in the internet and from the general fuzziness in thinking that both myself and my colleagues had when discussing this. The experiment consists of taking some handy items and rolling them down an inclined plane.

The genesis of this experiment was a high school physics experiment on rotational dynamics that my son was tasked to perform recently. I’ve always enjoyed rotational dynamics and, after we had discussed performing this particular experiment, I went to Home Depot and purchased some wood and metal rods and some metal tubes of various radii and lengths. I dutifully brought the booty home, pulled out a miter box and the appropriate saws, and cut the pieces to a common length. Of course, the length of a cylinder rolling down an inclined plane can’t possibly matter – reflect for a moment on whether one cylinder of length $$L$$ will go down the plane differently than two cylinders, side-by-side, of lengths $$L/2$$ – but I wanted to keep things simple. However, when we performed the experiment, the results were not what I expected. My son and I sat down and worked through the free-body diagram and reached an amazing realization that I will share.

The figure below shows the free-body diagram for any object with a circular cross section rolling down an inclined plane. The forces on the object are: the force due to gravity $$m \vec g$$ acting on the center of mass, the normal force $$\vec N$$ exerted on the object by the plane, and the frictional force $$f$$. These are shown as black arrows in the diagram. The coordinate system $$\{ \hat x, \hat y\}$$ is aligned with the inclined plane so that only the gravitational force needs to be resolved into components, the only relevant one being $$-m g \sin( \gamma ) \hat x$$, shown in gray.

Application of Newton’s second law gives

\[ – m a \hat x = – m g \sin ( \gamma ) \hat x + f \hat x \]

for the acceleration $$a$$ of the object down the inclined plane.

Since we’ve stipulated that the object will roll down the inclined plane, there is a natural relationship between the linear distance travelled $$s$$ and the amount the object has rotated $$\theta$$ that is given by

\[ s = \rho \, \theta \; , \]

where $$\rho$$ is the radius.

Taking the first and second derivatives of this relationship yields

\[ s = \rho \, \theta \implies \; v = \rho \, \omega \implies \; a = \rho \, \alpha \]

or

\[ \alpha = \frac{a}{\rho} \; .\]

Now, the torque needed to rotate the object so that it rolls down the plane is provided by the frictional force $$\vec f$$, which always acts tangentially so that

\[ \vec \tau = \vec r \times \vec f \implies \; \tau = \rho f \; .\]

The amount of angular acceleration $$\alpha$$ delivered by the torque is given by

\[ \tau = I \alpha \; ,\]

where $$I$$ is the moment of inertia of the object. There will be a lot more said about $$I$$ later on.

Equating these two expression for $$\tau$$ gives

\[ f = \frac{I \alpha}{\rho} \; .\]

Finally, substituting in the expression for $$\alpha$$ in terms of $$a$$ gives

\[ f = \frac{I a}{\rho^2} \; .\]

At this point, the magnitude of the frictional force has been expressed in terms of the linear acceleration of the object down the plane and in terms of the object’s properties, and so the frictional force can be eliminated from the application of Newton’s second law, leaving

\[ -m a = -m g \sin( \gamma ) + \frac{I a}{\rho^2} \; .\]

Note that the sign of the last term must be positive since $$\vec f$$ is in the positive $$\hat x$$ direction.

Now solve for the acceleration to get

\[ a = \frac{ g \sin( \gamma ) }{1 + \frac{I}{m \rho^2}} \; .\]

The final step is to relate the acceleration to the time it takes the object to descend the inclined plane under the constant acceleration determined above since that is the most convenient observable. Using the standard kinematic formula for motion under the influence of a constant acceleration and assuming the object starts at the top of the inclined plane at rest, the time it takes to reach the bottom, a distance $$L$$ from the top is

\[ t = \sqrt{ \frac{2 L}{ g \sin( \gamma ) } \left( 1 + \frac{I}{m \rho^2} \right) } \; .\]

A cursory glance at this formula would tend to coax one into the idea that an object with a larger moment of inertia would take a longer time descending the inclined plane. And this expectation seems to be widespread. For example, the article on calculating moments of inertia in Wikipedia has an animation showing a solid sphere, a solid cylinder, a spherical shell, and a cylindrical ring, all starting from rest at the top of an inclined plane. Each of these objects is released at the same time and they reach the bottom in the order listed in the previous sentence. The result of the animation is correct, but the caption is misleading. The author cites as reason that the resulting order depends on their moments of inertia. This is not true – the order depends only on the geometric distribution and has nothing whatever to do with the amount of matter contained in the object or with the size of the object.

To get a feel for why this result holds, consider a steel solid cylinder $$5 \, cm$$ long and $$0.5 \, cm$$ in radius. Assuming the density of steel to be $$8 \, g/cm^3$$, the mass of the cylinder is $$m = 31.4 \, g$$ and the moment of inertia is $$I = 3.9 \, g-cm^2$$. Now consider a steel tube of the same length with an inner radius $$\rho_1 = 0.4 \, cm$$ and an outer radius of $$\rho_2 = 0.5 \, cm$$. The mass and moment of inertia for the tube are $$m = 11.3 \, g$$ and $$I = 0.51 \, g-cm^2$$, respectively. The times for the two objects to descend a 1-meter long plane inclined at $$10 \, deg$$ are: $$t_{cylinder} = 1.33 \, s$$ and $$t_{tube} = 1.18 \, s$$. So, even though the cylinder has the greater mass (by a factor of 2.8) and moment of inertia (by a factor of 7.7), requiring a greater torque to set it rolling, it reaches the bottom first.

The key to understanding this result is to note that the moment of inertia enters in the equation in direct ratio to the $$m \rho^2$$. From dimensional grounds, the moment of inertia of any object rolling down the inclined plane must be

\[ I = k \, m \rho^2 \; , \]

where $$k$$ depends on the distribution of the matter but not on the amount or density. For common shapes, the moments of inertia (and correspondingly the values of $$k$$) are:

which explains the order shown in the Wikipedia article: $$k_{Solid Sphere} < k_{Solid Cylinder} < k_{Spherical Shell} < k_{Cylindrical Ring}$$. As an extreme case, consider a concrete pillar $$5 \, m$$ in radius with a mass of several metric tons and an acrylic tube with an outer radius of $$0.5 \, cm$$ and a thickness of $$0.1 \, cm$$ with a mass of a few grams. Set these objects at the top of the same inclined plane and allow them to descend from rest at the same time. The concrete pillar will reach the bottom first despite the fact that its moment of inertia dwarfs that of the plastic tube by maybe 15-20 orders of magnitude. Amazing, isn't it?