This month’s column is a departure from the norm but with good reason.  The usual fare consists of the development and subsequent mathematical exploration of some model of a physical phenomenon.  However, this installment serves more as a survey covering a broad swath of possible fluid phenomena rather than a detail exposition of each type of fluid behavior.  The reason for this quite simple: the possible types of fluid behavior is far more enormous than most of us ever realize.  It’s so vast that it seems that the terminology and classification has not kept pace with the discoveries as evidence by the tangled naming convention and the wide-spread confusion that exists on the internet (and often within related Wikipedia articles).

As school children, each of us is taught that there are three phases of matter: solid, liquid, and gas.  We are further taught that while solids have definite volume and shape, liquids only have definite volume, and gases do not enjoy certainty in either property.

If one pursues a STEM career in college, then a bit more information is added to these explanations and one learns that fluids are the collective name that we give for substances that ‘flow’ under stress.  Sometimes one even finds out that the key distinction between solids and fluids is that solids deform from their natural shape to a new shape under the application of a stress (typically leaving the volume unchanged or nearly so) but then return to their natural shape when the load is removed.  The amount of the deformation is determined by the magnitude of the load and, for ideal elastic solids, the relationship is linear, meaning that a double of the stress results in a doubling of the elastic strain.  In contrast, fluids do not have a natural shape (i.e. independent of their container) and so when a stress is applied, the material begins to flow with no terminal shape set by the magnitude of the load.  Removing the application of the load doesn’t mean that the fluid will return to its initial shape but rather that the flow will continue until internal frictional forces bring the flow to a halt.  These frictional forces are termed viscous forces and the degree to which they act in a fluid determines the fluid’s viscosity.

Now none of the above is untrue, in so far as it goes, but it tends to leave the idea that there is a sharp distinction between phases of materials.  And it is that is exactly what common sense and daily experience tell us is not true.

The world is literally littered with common materials that sometimes behave like a solid and sometimes like a fluid.  Consider the oobleck craze that swept across the internet some years back, which is nicely presented in the following video.

;

The two main ingredients are powdered cornstarch and water.  By themselves, each of these materials flow under stress and neither has a definite shape even if they both have definite volume.  But combine them together and suddenly one has a material that sometime behaves as a liquid, when the applied stress is low, and other times like a solid, when the applied stress is high.

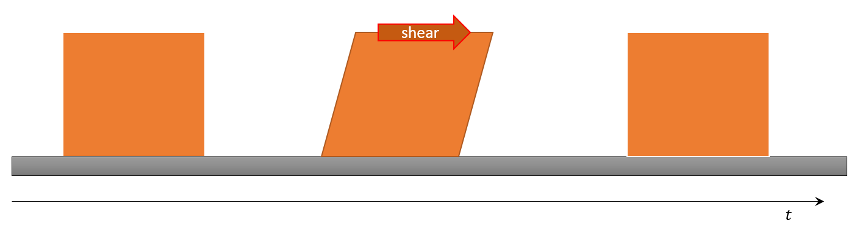
This behavior falls under the general heading of shear-thickening, the property whereby a fluid’s viscosity increases sharply as the applied stress increases.  An old school example of shear-thickening is Silly Putty, which is actually a viscoelastic material that behaves like an elastic solid on short time scales (it can holds its shape even while hammered and bounces nicely) but which flows slowly under low stress.

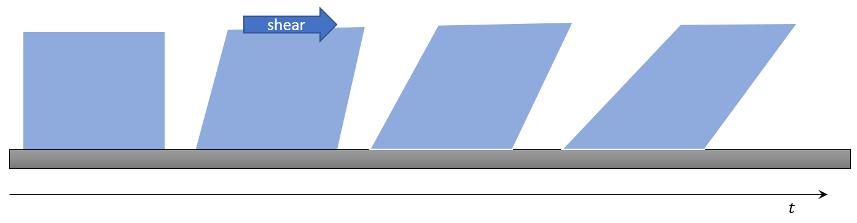
On the opposite side of the spectrum of flow behaviors is common household paint which flows far more easily when subject to the high stress as the brush or roller rub against the wall, allowing the paint to evenly wet the surface, but which becomes thicker under lower stress, allowing it to stay in place until it dries.  Many common kitchen items behave like this with ketchup

and whipped cream

being tasty examples.  Note how in the ketchup video, it flowed quite nicely when subjected to the high stress that resulted by pushing on the sides of the bottle but how it resisted gravity and crept at a much slower rate once it was in the glass.

Shear-thinning also can lead to some visually arresting behaviors like the Kaye effect in shampoo

Of course, not every material behaves like oobleck or Silly Putty or ketchup or shampoo.  Two of the most ubiquitous fluids, air and water, have constant viscosities (or nearly so) and their flow rate (i.e. strain rate) is proportional to the applied stress.

A general classification scheme exists that lumps all materials whose strain rate is proportional to the applied stress as Newtonian fluids and ‘all the others’ as non-Newtonian fluids.  And while the two most important fluids in our lives (at least external to our bodies) are Newtonian fluids, it seems pedagogically stunted to group the remaining fluids under the simple heading of non-Newtonian.  There are two broad categories under the non-Newtonian heading that were already discussed above:  shear-thickening and shear-thinning.  Graphically the differences between shear-constant (the name I argue should be attached to Newtonian fluids) and shear-thickening and -thinning are easily represented in the following diagram

The following table summarizes the various subcategories under shear-thinning and -thickening.

		Description	Examples	Applications
Shear thinning	pseudoplastic	shear viscosity decreases with applied stress in a time-independent way (𝜇=𝐾𝜖 ̇^(𝑛−1) with 𝑛<1)	Ketchup??, whipped cream, paint, blood	Commercial products, such as paint, where viscosity is low for application but high once applied
	thixotropic	shear viscosity decreases over time for a given stress; they thin when shaken	Paints, inks, solder pastes, thread-locking fluid, Ketchup??	Fisher Space Pen
Shear thickening	viscoelastic	Acts as a viscous liquid over long time scales but an elastic solid over short ones	Silly Putty, ligaments, tendons	Body armor, toys
	dilatant	shear viscosity increases with applied stress in a time-independent way (𝜇=𝐾𝜖 ̇^(𝑛−1) with 𝑛>1)	oobleck, wet sand, quicksand, silica within polyethylene glycol	Liquid body armor, brake pads, all wheel drive
	rheopectic	shear viscosity increases over time for a given stress; they thicken when shaken	Gypsum pastes, printer inks,	Body armor, shock absorption

It is interesting to note that even this categorization is rough and the lines between the groupings blur.  For example, the time-dependency exhibited by rheopectic and thixotropic materials may simply be masking a thermodynamic dependence.  No one is really sure.  That is why the very common material of ketchup is listed in both shear-thinning sub-categories.  And as the discussion about ketchup on rheothing.com shows the lines between them are fuzzy.

Next month’s column will look at the simplest fluid model, the Newtonian fluid.  The advantage of this simplicity is that we can construct an explicit model of the behavior.  The disadvantage is that much of the interesting phenomena that make the world fun to play in will have to wait.

This post is the first in what should be a fairly long sequence of articles concerning fluid mechanics.  The aim of this series is to present an intuitive feel for the phenomena of fluid mechanics from a physical point-of-view and a clean way of understanding the mathematical models used to describe them.  This last point deserves some comments especially.

One need only consult the numerous textbooks that abound in the marketplace of ideas to walk away with a profound sense of bewilderment at all the possible ways to express the fundamental, governing equations of fluid mechanics.  One’s confusion further increases by both a lack of standardization of terminology and by the failure to keep a sharp line between essential principles, such as the material derivative or the conservation of energy, and those relationships tailored for a specific application, such as the connection between applied stress and the strain rate for a Newtonian fluid.

This post attempts to improve this situation by deriving the governing equations, with no simplifications or specializations, using a minimalist approach consisting of the following ingredients:

1. The definition of the material derivative to move between the particle-flow (Lagrangian) and field (Euler) points-of-view (see Continuum Mechanics 1 – Material Derivative for details)
2. The divergence theorem
3. The Reynolds transport theorem connecting the time rate-of-change of a volume of fluid to its flow velocity (see Continuum Mechanics 3 – Reynolds Transport Theorem for details)
4. Surface forces defined in terms of the stress tensor
5. The conservation of mass
6. Newton’s second law
7. The First Law of Thermodynamics

This presentation reflects the influence of many sources, but the primary ones are Mechanics by Symon, The Governing Equations of Fluid Mechanics by Anderson found in Chapter 2 of Computational Fluid Mechanics, edited by Wendt, and An Introduction to Fluid Mechanics by Batchelor.  All of these are fine resources but each has a particular drawback that this synthesis is designed to address.

The governing equations of fluid mechanics in the particle-flow picture are particularly simple.  In this picture, we imagine looking as a small fluid element surrounded by either other fluid elements or boundaries with other materials.  By tracking the interactions of this element with its environment, one can easily write down the governing equations in familiar terms.  Transformation to the field picture is then facilitated by applying a combination of the items 1-3 in the list above.

Broadly speaking, there are two ways to combine items 1-3 to arrive at the field picture: the ordinary and flux-conservative forms (with many variations in each).  As discussed in detail in Anderson, the flux-conservative form, written generally as

\[ \frac{\partial \alpha}{\partial t} + \nabla \cdot \vec j_{\alpha} = 0 \; , \]

for a physical quantity $$\alpha$$ and corresponding current $$\vec j_{\alpha}$$ is the preferred form as it leads to better behaved equations, especially when dealing with shocks.   The ‘fork in the road’ between these two ways will be obvious below and will center on either explicitly using mass conservation in the equations (ordinary) or ignoring it (flux-conservative).

Conservation of Mass = Continuity Equation

The conservation of mass in the particle-flow picture is simply

\[ \frac{d}{dt} m = 0 \; ,\]

which states that, no matter how the boundary of the element deforms as it moves, the amount of matter contained within stays constant.

Defining the particle mass in the usual way, $$m = \rho {\mathcal Vol}$$, in terms of the mass density and the volume, gives

\[ \frac{d}{dt} \left( \rho {\mathcal Vol} \right) = \frac{d \rho}{dt} {\mathcal Vol} + \rho \frac{d}{dt} {\mathcal Vol} \; . \]

Next using Reynold’s transport theorem to eliminate the time derivative of the volume gives

\[ \frac{d \rho}{dt} {\mathcal Vol} + \rho \nabla \cdot {\vec V} \, {\mathcal Vol} = 0 \; . \]

The next step consists of using the form of the material derivative in the field picture to arrive at

\[ \left( \frac{\partial \rho}{\partial t} + {\vec V}\cdot \nabla \rho \right) {\mathcal Vol} + \rho \nabla \cdot {\vec V} \, {\mathcal Vol} = 0 \; .\]

Combining the second and the third term and then dividing out the $${\mathcal Vol}$$ gives the flux-conservative form of the continuity equation

\[ \frac{\partial \rho}{\partial t} + \nabla \cdot \left( \rho {\vec V}\right) = 0 \; . \]

Newton’s Second Law = Cauchy Momentum Equation

Newton’s second law in the particle-flow picture looks identical to how it is framed in elementary classical mechanics.

\[ \frac{d}{dt} \left( m \vec V \right) = \vec F_{total}\; , \]

where the right-hand side is the sum over all the forces exerted on the element.

Break the right-hand side into surface forces due to exchanges of momentum only at the boundary of the fluid element and body forces (e.g. gravity) where momentum exchange takes place between a field and every part of the element:

\[ \vec F_{total} = \sum_{faces} {\vec f}_s + {\vec f}_b {\mathcal Vol} \; .\]

Expressing the surface force on a given face in terms of the stress tensor as $${\vec f}_s = {\mathbf T} \cdot {\hat n} \, {\mathcal Area} $$, simplifies the first term to

\[ \sum_{faces} {\vec f}_s = \sum_{faces} {\mathbf T} \cdot {\hat n} \, {\mathcal Area} \; . \]

Applying the divergence theorem gives the final form of the resultant of the surface forces

\[ \sum_{faces} {\vec f}_s = \nabla \cdot {\mathbf T} \, {\mathcal Vol} \; .\]

Now examine the left-hand side first, which we will call $${\dot {\vec p }}$$.

\[ {\dot {\vec p }} = \frac{d}{dt} \left(m {\vec V} \right) = \frac{d m}{dt} {\vec V} + m \frac{d}{dt} {\vec V} \; . \]

There is a natural temptation to set the first term to zero and then to follow the same strategy as above.  Suppose this is done then

\[ \rho \, {\mathcal Vol} \frac{d}{dt} {\vec V} = \nabla \cdot {\mathbf T} \, {\mathcal Vol} + {\vec f}_b {\mathcal Vol} \; .\]

Dividing out the $${\mathcal Vol}$$ and expanding the material derivative gives

\[ \rho \left( \frac{\partial \vec V}{\partial t} + {\vec V} \cdot \nabla {\vec V} \right) = \nabla \cdot {\mathbf T} + {\vec f}_b \; . \]

While this is a valid fluid equation, it is not in flux-conservative form and, as cited above, experience has shown that the best equations for computational modeling are in flux-conservative form.  So we retain the $$(dm/dt) {\vec V}$$ and perform similar steps as to the above to get the left-hand side into the form

\[ \frac{d}{dt} {\vec p} = \frac{dm}{dt} {\vec V} + m \frac{d {\vec V}}{dt} = \left( \frac{\partial \rho}{\partial t} + \nabla \cdot {\rho {\vec V}} \right) {\vec V} {\mathcal Vol} \\ + \rho \, {\mathcal Vol} \left( \frac{\partial {\vec V}}{\partial t} + {\vec V} \cdot \nabla {\vec V} \right) \; . \]

Factoring out $${\mathcal Vol}$$ and combining terms yields

\[ \frac{d}{dt} {\vec p} = {\mathcal Vol} \left( \frac{\partial (\rho {\vec V})}{\partial t} + \nabla \cdot ({\rho {\vec V}{\vec V}}) \right) \; . \]

Substituting in this form and dividing out the volume gives the Cauchy momentum equation in flux form

\[ \frac{\partial (\rho {\vec V})}{\partial t} + \nabla \cdot ({\rho {\vec V}{\vec V}}) = \nabla \cdot {\mathbf T} + {\vec f}_b \; .\]

First Law of Thermodynamics = The Energy Equation

The final equation is the first law of thermodynamics, which in the particle-flow picture looks like

\[ \frac{d}{dt} E = \frac{d {\mathcal W}}{dt} + \frac{ d{\mathcal Q}}{dt} \; , \]

where $$E$$ is the total energy of the element, $$W$$ is the work done to the fluid element, and $$Q$$ is the heat that flows into it.  As in treatment of the Cauchy momentum equation, we need to distinguish between work due to surface forces and work due to body forces.  We must also distinguish between heat produced within the fluid element and heat that flows in from the boundary.

Because there are so many possible variations, we will content ourselves with one of the possible forms.  Additional posts will explore other forms of this equation and additional assumptions.

To start, let’s look at the left-hand side.  The total energy is the sum element’s kinetic energy and its internal potential energy

\[ E = \frac{1}{2} m {\vec V}^2 + U \; .\]

Defining the total energy through the relation $$E = m e_t$$ with the specific total energy $$e_t = V^2/2 + u$$, we can express the left-hand side as

\[ \frac{d}{dt} E = \frac{d}{dt} \left( m e_t \right) = \frac{dm}{dt} e_t + m \frac{d e_t}{dt} \; .\]

As in the case of the momentum equation, keeping the time-derivative of mass explicitly around leads to the flux-conservative form.  This is done with the usual application of the Reynold’s transport theorem and the definition of the material derivative to arrive at

\[ \left[ \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec V) \right] e_t {\mathcal Vol} + \rho {\mathcal Vol} \left[ \frac{\partial e_t}{\partial t} + {\vec V} \cdot \nabla (e_t) \right] \; . \]

These two terms combine nicely to yield

\[ \left[ \frac{\partial \rho e_t}{\partial t} + \nabla \cdot (\rho e_t \vec V) \right] {\mathcal Vol} \; , \]

for the left-hand side.

Over on the right-hand side the time rate of work done is given by

\[ \frac{d W}{dt} = \vec F_{total} \cdot \vec V = \vec f_{body} \cdot \vec V \, {\mathcal Vol} + \sum_{faces} \vec f_{s} \cdot \vec V \; .\]

The last term can be put into a more useful form by again expressing the surface forces in terms of the stress tensor to get that the work done by these forces is then

\[ \sum_{faces} \vec f_s \cdot \vec V = \sum_{faces} ({\mathbf T} \cdot \vec V ) \cdot {\hat n} \, {\mathcal Area} \; .\]

Finally apply the divergence theorem to get

\[ \sum_{faces} \vec f_s \cdot \vec V = \nabla \cdot ({\mathbf T} \cdot \vec V ) {\mathcal Vol} \; ,\]

which, when substituted back, gives a final form for the rate of work performed of

\[ \frac{d W}{dt} = \left[ \vec f_{body} \cdot \vec V + \nabla \cdot ({\mathbf T} \cdot \vec V ) \right] {\mathcal Vol} \; .\]

The rate of change in the heat in the element is given by

\[ \frac{dQ}{dt} = \rho \dot q {\mathcal Vol} + \sum_{faces} \vec h \cdot \hat n {\mathcal Area} \; , \]

where the first term accounts for the volumetric heating occurring within the element and the second term represents the heat flux $$\vec h$$ entering through the faces.

Applying the divergence theorem to the last term gives a final form for the rate of change of the heat of

\[ \frac{dQ}{dt} = \left[ \rho \dot q + \nabla \cdot \vec h \right] {\mathcal Vol}\; . \]

Equating all of these pieces and dividing out the volume yields the general form of the energy equation in flux-conservative form

\[ \frac{\partial \rho e_t}{\partial t} + \nabla \cdot (\rho e_t \vec V) = \vec f_{body} \cdot \vec V + \nabla \cdot ({\mathbf T} \cdot \vec V ) + \rho \dot q + \nabla \cdot \vec h \; . \]

Next month’s columns will begin to look at specific physical solutions to this equations in simple settings.

This installment was intended to be a realigning of the recent series of articles on continuum mechanics to a set of columns specialized to fluid mechanics.  However, there is a nice derivation of the inner workings of the stress tensor that I developed while working on the new post on fluids that is worthy of some daylight.  In some sense, this post (and the one that follows) adds the rigor that was missing from the general discussion presented in the column entitled Continuum Mechanics 5 – The Stress Tensor.  So, this month’s offering is a complete rederivation of a coordinate-free representation of the stress tensor.

As discussed in that earlier post, the force on a surface is naturally a function of the surface normal.  What was taken on authority was that the mapping should be linear (i.e., tensorial) and symmetric in order that there be no unphysical translational and angular accelerations, respectively.  This post will prove that the mapping should be linear, and next month’s post will provide a rigorous derivation of the symmetry properties.

All that is needed to construct a mathematical derivation are some basic physical principles and elementary mathematics.  The starting point for the derivation is Cauchy’s tetrahedron,

a portion of the continuum where three sides of the figure (denoted by the superscripts $$(1), (2), (3)$$)  coincide with coordinate planes (i.e., $$x$$-$$y$$, $$y$$-$$z$$, and $$z$$-$$x$$ planes) and the fourth side (no superscript) closes the shape.

The physical principles that we will employ are Newton’s laws, the fact that the surface force across an interface is proportional to the area of the interface, and the fact that the volume scales as the cube of some characteristic length $$L$$ while the area scales as the square.

Newton’s second law applied to the tetrahedron yields

\[ m_{T} \, {\vec a}_{T} = {\vec f}^{(1)} + {\vec f}^{(2)} + {\vec f}^{(3)} + {\vec f} \equiv {\vec f}_{total} \; ,\]

where $$m_{T}$$ is the mass of the tetrahedron and $${\vec a}_{T}$$ is the acceleration. Since the mass of the tetrahedron is the product of the mass density times the volume, $$\rho {\mathcal V}_T$$, it scales as $$\alpha^3$$ as each linear dimension is scaled by a factor $$\alpha$$.  Each of the forces on the right-hand side is proportional to an area of the face (e.g., $${\vec f}^{(1)} \propto \delta S^{(1)}$$), it scales as $$\alpha^2$$ as each linear dimension is scaled by the same factor $$\alpha$$.

The entire equation, when subjected to this scaling, becomes

\[ m_{\mathcal T} \, \alpha^3 \, {\vec a}_{T} = \alpha^2 {\vec f}_{total} \; .\]

Dividing through by $$\alpha$$, gives the acceleration as

\[ {\vec a}_{T} = \frac{1}{\alpha \, m_{T}} {\vec f}_{total} \; .\]

In order to prevent an infinite acceleration as $$\alpha \rightarrow 0$$, we require that the forces exactly balance to zero.

\[ {\vec f}_{total} = {\vec f}^{(1)} + {\vec f}^{(2)} + {\vec f}^{(3)} + {\vec f} = 0 \; .\]

Now we want to characterize the forces.  Since we know that each force is proportional to the area and depends on the normal we can write the mapping generally as

\[ {\vec f}^{(i)} = {\mathbf T}\left({\hat n}^{(i)}\right) \delta S^{(i)} \; , \]

for $$i = 1, 2, 3$$ and ‘blank’ (that is, no superscript for the oblique face).

From Newton’s third law, we know that the force on one side of an interface must be equal and opposite to the force on the other side.  This relationship requires that

\[ {\mathbf T}({\hat n}) = – {\mathbf T}({\hat n}) \; . \]

By their orientation, the faces that coincide with a coordinate plane have unit normals that relate to the basis vectors as

\[ {\hat n}_1 = – {\hat e}_1 \; , \]

\[ {\hat n}_2 = – {\hat e}_2 \; , \]

and

\[ {\hat n}_3 = – {\hat e}_3 \; . \]

From basic geometry, the areas of each of these planes are related to the area of the fourth plane by

\[ \delta S_1 = {\hat n} \cdot {\hat e}_x \, \delta S \; , \]

\[ \delta S_2 = {\hat n} \cdot {\hat e}_y \, \delta S \; , \]

and

\[ \delta S_3 = {\hat n} \cdot {\hat e}_z \, \delta S \; . \]

Since the set $$\{{\hat e}_x, {\hat e}_x, {\hat e}_x,\}$$ spans the space, the normal to the oblique face can be decomposed as

\[ {\hat n} = ({\hat e}_x \cdot {\hat n}) {\hat e}_x + ({\hat e}_y \cdot {\hat n}) {\hat e}_y + ({\hat e}_z \cdot {\hat n}) {\hat e}_z \equiv a \, {\hat e}_x + b \, {\hat e}_y + c \, {\hat e}_z \; . \]

Returning to the force equilibrium, and expressing the forces in terms of the stress and areas, and the areas of the faces aligned with the coordinate planes in terms of the area of the oblique face, yields

\[ {\mathbf T}({\hat n}) \, \delta S = – {\mathbf T} \left( {\hat n}^{(1)} \right) \, ({\hat e}_x \cdot {\hat n} ) \, \delta S \\ – {\mathbf T} \left( {\hat n}^{(2)} \right) ({\hat e}_y \cdot {\hat n} ) \, \delta S \\ – {\mathbf T} \left({\hat n}^{(3)} \right) ({\hat e}_z \cdot {\hat n} ) \, \delta S \; . \]

Divide out the common factor of $$\delta S$$, replace the dot products of the normal with the basic vectors by the components, and exploit Newton’s third law to absorb the minus signs on the right-hand side

\[ {\mathbf T}({\hat n}) = a {\mathbf T} \left({\hat e}_{x}\right) + b {\mathbf T} \left({\hat e}_{y}\right) + c {\mathbf T} \left({\hat e}_{z}\right) \; . \]

Finally, substitute in the form of the normal into the left-hand side to get

\[ {\mathbf T}\left( a {\hat e}_x + b {\hat e}_y + c {\hat e}_z \right) = a {\mathbf T} \left({\hat e}_{x}\right) + b {\mathbf T} \left({\hat e}_{y}\right) + c {\mathbf T} \left({\hat e}_{z}\right) \; . \]

The foregoing result is the definition of a tensorial relationship, and the first half of the proof is complete.

This month’s post marks the end of the study of continuum mechanics, or rather it marks the end of the name.  The past nine posts have focused on the basic material common to elasticity and fluids and then moved into a brief study of elastic motion.  The material here will serve as the final post on elasticity, cleaning up some loose ends and providing some rigor.  Next month, the focus will turn to fluid mechanics and the series will be retitled and renumbered accordingly.

The three topics covered here provide some additional details and rigor to the discussions that have come before with a particular focus on the elastic equations of motion that are used to analyze the wave motion discussed in post 9.

Rigorous derivation of the strain tensor

When I was first exposed to elasticity, it was from Chapter 3 of Mathematical Methods, 3^rd edition by Arfken; and, in fact, I used that text as a guide for the material in post 7.  However, a brief consultation with more specialized texts will often yield a strain tensor that is a bit more complex than the one presented in either of those two sources.  A more complete derivation, which is patterned after the derivation here, supplemented with my own insights, is as follows.

Let the position of any point at any stage of the deformation be defined by $${\vec r}_t = \vec \phi (\vec r, t)$$,  where $$\vec r$$ is the initial position of the point and $$t$$ measures the extent of deformation.  The function $$\vec \phi(\vec r,t)$$ is called the flow mapping.  The parameter $$t$$ parameterizes the deformation, labeling the successive stages.  It doesn’t necessarily need to be regarded as the time but it is often convenient to treat it as such and it will used that way below.  The requirement that $$\vec r$$ is the original undeformed position imposes the obvious boundary: $$\vec \phi (\vec r, 0) = \vec r$$.

Now focus on two points $${\mathcal P}$$ and $${\mathcal Q}$$ before and after the derivation.   Their positions before the deformation are:

\[ \vec {\mathcal P}(0) = \vec \phi(\vec r,0) = \vec r \; \]

and

\[ \vec {\mathcal Q}(0) = \vec \phi(\vec r + d \vec r,0) = \vec r + d \vec r \; . \]

After the deformation, the same two points are now located at

\[ \vec {\mathcal P}(t) = \vec \phi(\vec r, t) \; \]

and

\[ \vec {\mathcal Q}(t) = \vec \phi(\vec r + d \vec r,t) = \vec \phi(\vec r,t) + \frac{\partial \vec \phi(\vec r, \epsilon) }{\partial \vec r} d \vec r \; , \]

where the assumptions that $$d \vec r$$ is small in magnitude and that $$\vec \phi$$ is differentiable have been made.

Now measure the distance between the points $${\mathcal P}$$ and $${\mathcal Q}$$.  Before the deformation, that distance squared is given by

\[ ds^2 = \left\Vert \vec {\mathcal P}(0) – \vec {\mathcal Q}(0) \right \Vert^2 = d \vec r \cdot d \vec r = d r_i d r_i \; . \]

After the deformation, the distance squared between those points, now moved to their new position, is given by

\[ ds_{t}^2 = \left\Vert \vec {\mathcal P}(t) – \vec {\mathcal Q}(t) \right \Vert^2 = \frac{\partial \phi_i}{\partial r_j} d r_j \frac{\partial \phi_i}{\partial r_k} d r_k \; . \]

Calculate the difference between these two lengths

\[ ds_{t}^2 – ds^2 = \frac{\partial \phi_i}{\partial r_j} d r_j \frac{\partial \phi_i}{\partial r_k} d r_k – d r_j d r_k \delta_{jk} = \left( \frac{\partial \phi_i}{\partial r_j} \frac{\partial \phi_i}{\partial r_k} – \delta_{jk} \right) dr_j dr_k\; ,\]

where the last term has been modified a bit by the inclusion of a Kronecker delta.

We now define the Green-Lagrange strain tensor by the relationship

\[ 2 \epsilon_{jk} = \frac{\partial \phi_i}{\partial r_j} \frac{\partial \phi_i}{\partial r_k} – \delta_{jk} \; .\]

The strain vector $$\vec u$$ measures the difference in position between where a particle originally was located and where it is located at time $$t$$

\[ \vec u(t) = \vec \phi(\vec r,t) – \vec r \; . \]

Spatial derivatives of $$\vec \phi$$ are related to spatial derivatives of the deformation vector $$u$$ via

\[ \frac{\partial \phi_i(\vec r,t)}{\partial r_j} = \delta_{ij} + \frac{\partial u_i}{\partial r_j} \; . \]

Substituting this expression into the Green-Lagrange strain tensor gives

\[ 2 \epsilon_{jk} = \left( \delta_{ij} + \frac{\partial u_i}{\partial r_j} \right) \left( \delta_{ik} + \frac{\partial u_i}{\partial r_k} \right) – \delta_{jk} \; . \]

Expanding and simplifying yields

\[ \epsilon_{jk} = \frac{1}{2} \left( \frac{\partial u_k}{\partial r_j} + \frac{\partial u_j}{\partial r_k} + \frac{\partial u_i}{\partial r_j}\frac{\partial u_i}{\partial r_k} \right) \; , \]

which is the same as the earlier derivation except for the nonlinear term that can often be dropped.

Rigorous derivation of the equations of motion

The same notions can be used to derive the equations of motion that led to the wave equation analyzed in the last post.  Consider a cube of the continuum centered at $$\vec r$$.

The force on any face is given by $$f_i = T_{ij} n_j Area$$.  Start first with the forces on the two faces perpendicular to the $$x$$-axis.  The center of the rightmost face is located at $$\vec r + (\delta x/2) \hat \imath$$ and it is at this point that the stress is evaluated.  Likewise, the center of the leftmost face lies at $$\vec r – (\delta x/2) \hat \imath$$.  For notational convenience, functions evaluated on the rightmost face will be denoted with the argument $$x_{+}$$ and those evaluated on the leftmost face with $$x_{-}$$.  In this notation, the components of the forces on these faces are:

\[ \left[ \begin{array}{c} f_x \\ f_y \\ f_z \end{array} \right] = \left[ \begin{array}{c} T_{xx}(x_+) – T_{xx}(x_-) \\ T_{yx}(x_+) – T_{yx}(x_-) \\ T_{zx}(x_+) – T_{zx}(x_-) \end{array} \right] dy dz = \left[ \begin{array}{c} T_{xx,x}(\vec r) \\ T_{yx,x}(\vec r) \\ T_{zx,x}(\vec r) \end{array} \right] dx dy dz \; , \]

where the last equalities result by taking a Taylor’s expansion of the finite difference and keeping terms of only first order ($$T_{ij,k} = \partial T_{ij} / \partial r_k$$).

Similar manipulations give the expressions

\[ \left[ \begin{array}{c} f_x \\ f_y \\ f_z \end{array} \right] = \left[ \begin{array}{c} T_{xy}(y_{+}) – T_{xy}(y_-) \\ T_{yy}(y_+) – T_{yy}(y_-) \\ T_{zy}(y_+) – T_{zy}(y_-) \end{array} \right] dx dz = \left[ \begin{array}{c} T_{xy,y}(\vec r) \\ T_{yy,y}(\vec r) \\ T_{zy,y}(\vec r) \end{array} \right] dx dy dz \; \]

and

\[ \left[ \begin{array}{c} f_x \\ f_y \\ f_z \end{array} \right] = \left[ \begin{array}{c} T_{xz}(z_+) – T_{xz}(z_-) \\ T_{yz}(z_+) – T_{yz}(z_-) \\ T_{zz}(z_+) – T_{zz}(z_-) \end{array} \right] dx dy = \left[ \begin{array}{c} T_{xz,z}(\vec r) \\ T_{yz,z}(\vec r) \\ T_{zz,z}(\vec r) \end{array} \right] dx dy dz \; , \]

for the components of the force generated on the $$y$$- and $$z$$-faces, respectively.

Combining these results and expressing the sums in index notation gives the final, compact expression for the force as

\[ f_i = T_{ij,j} dx dy dz \; .\]

Note that the mass of the continuum contained in the cube is $$\rho \, dx dy dz$$, where $$\rho$$ is the mass density.  Newton’s second law for the cube then relates the acceleration of the cube, which is expressed in terms of the second time-derivative of the flow mapping to the cube’s mass and the forces acting on the cube as

\[ (\rho \, dx dy dz) \frac{\partial^2 \phi(\vec r,t)}{\partial t^2} = f_i \; . \]

Using the relation between the flow mapping and the deformation vector and between the force and the stress tensor gives

\[ \rho \, \partial^2_t u_i = T_{ij,j} \; , \]

which is precisely the starting expression for the last post.

Relation between the Lame constants and the elastic moduli

This final section derives the relationships to express the elastic moduli derived in post 7 to the Lame constants, which were introduced as a shorthand for the wave equation in an isotropic medium.  The Lame constants took the form

\[ \lambda = \frac{\nu E}{(1+\nu)(1-2\nu)} \; \]

and

\[ \mu \frac{E}{2(1+\nu)} \; ,\]

where $$E$$ is Young’s modulus and $$\nu$$ is Poisson’s ratio.

It is a matter of some simple algebra to express Young’s modulus and Poisson’s ration in terms of $$\lambda$$ and $$\mu$$ as follows.  Manipulating the second equation gives  $$E = 2 (1+\nu) \mu$$.  Substituting this into the first equation gives $$\lambda = 2 \nu \mu / (1-2\nu)$$ from which one gets via simplification

\[ \nu = \frac{\lambda}{2 (\mu + \lambda) } \; . \]

Back-substituting gives

\[ E = \mu \frac{2\mu + 3 \lambda}{\mu + \lambda} \; \]

for Young’s modulus.

To relate the shear and bulk moduli to the Lame constants, return to the generalized Hooke’s law

\[ T_{ij} = 2 \mu \epsilon_{ij} + \lambda Tr(\epsilon) \delta_{ij} \; . \]

In the case of an isolated shear along the $$x$$-direction that grows along the $$y$$-direction, the strain is expressed as $$\partial_y u_x$$ and the only non-zero terms in the strain tensor are $$ \epsilon_{xy} = \epsilon_{yx} = 1/2 \, \partial_y u_x$$.  Thus,

\[ T_{xy} = 2 \mu \epsilon_{xy} = 2 \mu \frac{1}{2} \partial_y u_x = \mu \partial_y u_x \; .\]

Since the shear modulus is defined (see post 8) as the ratio of stress $$T_{xy}$$ and the strain $$\partial_y u_x$$, it is clear that $$G = \mu$$.

Finally, the bulk modulus applies when the continuum is in isotropic (i.e. hydrostatic) stress equilibrium.  Isotropic stress means that the strain tensor is diagonal with all its on-diagonal components equal: $$T_{xx} = T_{yy} = T_{zz} \equiv T_{iso}$$.  The strain tensor is also diagonal with $$\epsilon_{xx} = \epsilon_{yy} = \epsilon_{zz} \equiv \epsilon_{iso}$$.  The application of $$T_{iso}$$ represents a pressure that uniformly compresses the continuum.  The measure of that compression is given by the fractional change in volume.  Consider a small cube of initial length $$L$$ on a side so that applying $$T_{iso}$$ causes an isotropic strain of $$\Delta L$$ in all directions.  The volume before the strain is $$L^3$$ and the volume after is, to first order, $$L^3 – 3 L^2 \Delta L$$.  The fractional change in the volume is then

\[ \frac{\Delta V}{V} = -\frac{3 L^2 \Delta L}{L^3} = -3 \frac{\Delta L}{L} = -3 \epsilon_{iso} \; . \]

The bulk modulus is defined as the ratio

\[ K = -\frac{\Delta P}{\Delta V/V} = \frac{T_{iso}}{3 \epsilon_{iso}} \; .\]

From the generalize Hooke’s law

\[ T_{iso} = 2 \mu \epsilon_{iso} + \lambda 3 \epsilon_{iso} = (2 \mu + 3 \lambda) \epsilon_{iso} \; . \]

Comparing the two expressions gives

\[ K = \lambda + \frac{2}{3} \mu \; . \]

So, that’s it for now on elastic solids and that corner of continuum mechanics.  Next month, I turn towards the related subdiscipline of fluid mechanics.

Last month’s post set the stage for one of the more interesting and important aspects of elastic motion – the propagation of elastic deformation waves in a material.  The familiar travelling and standing waves seen on stringed instruments are the prototype example but the richness and complexity is increased when the allowed deformations take place in more dimensions.  The complex relationship of the generalized Hooke’s law relating the strain to the stress tensor given by

\[ T_{ij} = c_{ijkl} \epsilon_{kl} \; ,\]

leads to many more propagation modes compared to the one-dimensional textbook case.  Since every solid material can support elastic waves, understanding these modes becomes important in the mechanical design of all manner of objects, such as bridges, support columns, cars, planes, skyscrapers, and so on.  This analysis also serves as a cornerstone in seismology for understanding one of the most powerful and catastrophic events on the planet, the earthquake.

As discussed in the last post, there are 81 components in the stiffness tensor $$c_{ijkl}$$ but there are never more than 21 independent components due to various symmetries of the physical relationships connecting the stiffness tensor to the stress and strain tensors.  This is a substantial reduction but is still far too complicated for an initial foray into elastic waves so the first step is to look at the waves that arise in an isotropic medium.

To perform this analysis requires three steps.  The first step simplifies the generalized Hooke’s law in terms of the elastic moduli discussed in detail in the previous post.   The second step adapts Newton’s law for the elastic medium yielding the wave equation.  The last step is the decomposition of the wave equation into its independent components.

Step 1 – Simplifying Generalized Hooke’s Law

To simplify the generalized Hooke’s law for an isotropic material begin by focusing in on the strains that result along the $$x_1$$-axis as a result of the application of various stresses.  Applying a small tensile stress along the $$x_1$$-axis gives

\[ E \epsilon_{11} = T_{11} \; , \]

where $$E$$ is Young’s modulus.

Application of the same small tensile stress along the $$x_2$$- and $$x_3$$-axes yields

\[ -\frac{E}{\nu} \epsilon_{11} = T_{22} \; \]

and

\[ -\frac{E}{\nu} \epsilon_{11} = T_{33} \; , \]

where $$\nu$$ is Poisson’s ratio.  Note that no indices are needed on this Poisson’s ratio since the material is isotropic.

Putting these pieces together gives

\[ E \epsilon_{11} = (1+\nu) T_{11} – \nu \left(T_{11} + T_{22} + T_{33} \right) = (1+\nu) T_{11} + \nu Tr({\mathbf T}) \; ,\]

where $$Tr({\mathbf T})$$ is the trace of the stress tensor.

Arfken presents a rigorous argument for generalizing the above equation but it is obvious that it is consistent with the form

\[ E \, \epsilon_{ij} = (1+\nu) T_{ij} – \nu Tr({\mathbf T}) \delta_{ij} \; . \]

Taking the trace of both sides and performing some straightforward algebra gives

\[ T_{ij} = \left( \frac{E}{1+\nu} \right) \epsilon_{ij} + \left(\frac{\nu}{1+\nu}\right) \left(\frac{E}{1-2\nu}\right) Tr({\mathbf \epsilon}) \delta_{ij} \; . \]

It is traditional to recast this equation slightly by defining the Lame coefficients

\[ \lambda = \frac{\nu E}{ (1+\nu)(1-2\nu) } \; ,\]

and

\[ \mu = \frac{E}{2 (1+\nu)} \; .\]

The isotropic stress-strain relationship now takes on the compact form

\[T_{ij} = 2 \mu \epsilon_{ij} + \lambda Tr({\mathbf \epsilon}) \delta_{ij} \; , \]

which is the desired relation.

Step 2 – Adapting Newton’s Law

The next step is to adapt Newton’s law to a piece of the continuum.  The standard way of doing this is to look at a small cube of the continuum whose sides are spanned by the components $$u_i$$, similar defined as in the earlier post in which the strain tensor is first derived.  The resulting equation is then (see https://www.geophysik.uni-muenchen.de/~igel/Lectures/Sedi/sedi_weq.pdf)

\[ \rho \partial_t^2 u_i = T_{ij,j} \; .\]

Substituting in for $$T_{ij}$$ with the relationship from step 1 yields

\[ \rho \partial_t^2 u_i = \partial_j \left( 2 \mu \epsilon_{ij} + \lambda Tr({\mathbf \epsilon}) \delta_{ij} \right) \; .\]

By definition of the strain tensor

\[2 \epsilon_{ij} = \partial_i u_j + \partial_j u_i \; \]

and

\[ Tr({\mathbf \epsilon}) = \partial_k u_k \; . \]

Substituting these definitions in yields

\[ \rho \partial_t^2 u_i = \lambda \partial_i \partial_k u_k + \mu \partial_i \partial_j u_j + \mu \partial^2_j u_i \; .\]

In vector terms

\[ \rho \partial_t^2 {\vec u} = (\lambda + \mu) \nabla (\nabla \cdot \vec u) + \mu \nabla^2 \vec u \; . \]

Step 3 – Decomposing the Wave Equation

As it stands the, wave equation mixes the various independent modes.  This observation isn’t at all obvious but it will become apparent with the application of the vector identity

\[ \nabla^2 \vec u = \nabla(\nabla \cdot \vec u) – \nabla \times (\nabla \times \vec u) \; .\]

Substituting this relation into the wave equation and collecting terms gives a new form of the wave equation

\[ \rho \partial_t^2 \vec u = (\lambda + 2 \mu) \nabla (\nabla \cdot \vec u) – \mu \nabla \times (\nabla \times \vec u) \; .\]

The importance of this form is that there are now two uncoupled modes: the ‘divergence’ mode and the ‘curl’ mode.  To see this, take the divergence of both sides and exchange all partial derivatives with abandon.  Since the divergence of a curl is identically zero the result is

\[ \rho \partial_t^2 \nabla \cdot \vec u = (\lambda + 2 \mu) \nabla^2 (\nabla \cdot \vec u) \; .\]

From this equation, we can see that a compression/expansion wave propagates with a speed given by

\[ v_{P} = \sqrt{ \frac{\lambda + 2 \mu}{\rho} } \; . \]

The ‘P’ label stands for primary or pressure wave.

Likewise, taking the curl gives

\[ \rho \partial_t^2 \nabla \times \vec u = \mu \nabla^2 (\nabla \times \vec u) \; .\]

From this equation, we can see that a shear wave propagates with a speed given by

\[ v_{S} = \sqrt{ \frac{\mu}{\rho} } \; . \]

The ‘S’ label stands for secondary or shear wave.

As the links to Wikipedia show, this simple theory has been used to analyze earthquake propagation.

 

The last post introduced the idea of the deformation field $${\vec u}(\vec r)$$ and the corresponding strain tensor $$2\epsilon_{ij} = \partial_j u_i + \partial_i u_j$$, which characterizes the amount that any two points in the continuum move away from each other.

While formally correct, the mathematical form of the strain tensor tends to obscure any physical intuition as to what different components are all about.  Some small hint for how to interpret the strain tensor was touched upon in the closing of the last post.  This post provides a more in-depth coverage by introducing the elastic moduli.

The elastic moduli generalize the concept of a spring concept from elementary mechanics.  Roughly speaking, these numbers describe the resistance that the material has to one of three basic actions:  1) Young’s modulus (usually called $$E$$) – being stretched or compressed along a particular direction, 2) bulk modulus (usually called $$K$$) – being expanded or contracted in all directions, and 3) shear modulus (usually called $$G$$) – being sheared.  The primary distinction between 1) and 2) is that the density of the material need not change during a uniaxial deformation but must necessarily change for a full expansion or contraction.  Detail for each of these follows.

Youngs Modulus

Consider a uniform rod of material of a rectangular cross-section $$A$$ with a natural length (i.e. stress-free) $$L$$.  When subjected to a tension force $$F$$, the rod expands by $$\Delta L$$.

Measurements of the extent of the stretch as a function of the stress gives Young’s modulus as

\[ E = \frac{F/A}{\Delta L/L} = \frac{T_{xx}}{\epsilon_{xx}} \; , \]

where the last equality follows by defining the long axis of the bar as the $$x$$-axis and $$T_{xx}$$ and $$\epsilon_{xx}$$ are the corresponding components of the stress and strain tensors.

Interestingly, the story of uniaxial stress isn’t quite complete.  As anyone who has every play with rubber bands knows, when an elastic material lengthens in one direction it typically shrinks in the transverse directions; the band gets thinner in the two directions perpendicular to the ‘stretch’ direction.

Generally, the transverse directions do not shrink by the same amount since the degree of contraction depends on material composition and this difference is manifest in $$\Delta L’ \neq \Delta L”$$.  Poisson’s ratios are defined as

\[ \nu_{zx} = -\frac{\Delta L’}{\Delta L} \; \]

and

\[ \nu_{zy} = -\frac{\Delta L”}{\Delta L} \; ,\]

where the notation $$\nu_{ij}$$ measures the ratio of change along the $$j$$-axis as a function of the strain caused along the $$i$$-axis by the corresponding stress.

When $$\Delta L’ = \Delta L”$$ the material has an axis of symmetry about which there is an axial uniformity.  If Young’s modulus is the same in all direction, then the material is called isotropic and no indices are needed as there is only one Poisson’s ratio needed.  The assumption of isotropy works for many simple materials but certain elastic man-made materials have very directionally-dependent Poisson ratios.   The Wikipedia article on Poisson’s ratio lists six separate ratios $$\nu_{ij}$$ for the fabric Nomex.

Note that as the material undergoes its elongation and retraction in the direction of the stress and in the perpendicular directions, respectively, that the density can remain constant or that it change.  The exact determination depends on the material as does just how much the two perpendicular directions differ in the amount they contract.

Bulk Modulus

Consider a small unit of material suddenly placed inside a high-pressure environment.  An example would be the submergence of a metal cube at the bottom of the ocean.  Compression stress assaults the cube from all sides seeking to change the volume and, hence, the density of the material.

The bulk modulus measures how resistant the material is to this change and, defined as the ratio of the pressure $$P$$ to the fractional change in the volume $$\Delta V / V$$, becomes

\[ K = – \frac{\Delta P}{\Delta V/V} \approx -V \frac{d P}{d V} ; .\]

Shear Modulus

Consider a rod of material that is placed between two plates, the bottom one fixed and the top one free to move along the $$x$$-direction.  As it moves, the top plate exerts a stress $$T_{xy}$$ on the top face of area $$A$$, which deforms the material by varying degrees as a function of distance $$y$$ from the fixed plate.

If the height of the rod is $$L$$ and the amount of deformation at the top is $$\Delta x$$ then the shear modulus is defined as

\[ G_{xy} = \frac{F/A}{\Delta x/L} = \frac{T_{xy}}{\partial_y u_{x}} = \frac{T_{xy}}{2 \epsilon_{xy}} \; . \]

Similar expressions exist for the other possible combinations of directions.  An isotropic material needs only one shear modulus to describe it.

General Relation of Strain to Stress

The definitions of the three basic moduli relate strain to stress in an intuitive and geometric way but the tensor nature of the stress and strain are absent and any connection between the moduli are obscure at this point.  The final step is to synthesize them into a general relationship between the stress tensor $$T_{ij}$$ and the strain relationship $$2 \epsilon_{ij}$$ and to discover how the moduli connect to each other.

The full tensor relationship is given by the generalize Hooke’s law

\[ T_{ij} = c_{ijkl} \epsilon_{kl} \; , \]

where the fourth-rank stiffness tensor $$c_{ijkl}$$ plays the role of the spring constant in the simply form of Hooke’s law $$F = -k x$$.   There are 81 different components of the stiffness tensor but most of them are not independent.  The symmetric nature of the stress and strain tensors ($$T_{ij} = T_{ji}$$ and $$\epsilon_{ij} = \epsilon_{ji}$$) imposes the relationships

\[ c_{ijkl} = c_{jikl} = c_{ijlk} = c_{jilk} \]

reducing the number of independent components to 36.  A further reduction down to 21 independent components comes from noting that the stiffness matrix is also symmetric upon the interchange of the first and second pair of indices

\[ c_{ijkl} = c_{klij} \; .\]

This symmetry in the stiffness tensor is inherited from the potential energy for an elastic body

\[ PE = \frac{1}{2} c_{ijkl} \epsilon_{ij} \epsilon_{kl} \; , \]

which is clearly invariant under the exchange of $$\epsilon_{ij}$$ and $$\epsilon_{kl}$$.

Next month’s column focuses on isotropic materials, exploring the specific relationships between the moduli in this case, and by looking at how elastic waves propagate.

As part of the series on Continuum Mechanics, this post is the first of several focusing on elastic behavior of materials. Referring to the previous post, elastic materials are ones which, in contrast with fluids, deform under the application of a stress but return to their equilibrium shape upon the removal of the stress.

Before characterizing the strain mathematically, consider first some physical expectations from the simple bending of a beam under the load. To focus the discussion, look at the three specific points in orange, yellow, and black.

Prior to the deformation, the separation between the orange and yellow points is entirely along the horizontal, and the separation between the yellow and black points is entirely along the vertical. Denote the relative position of the orange point relative to the yellow as $$\delta {\vec r}_0$$ and then examine what happens to that relative position under a load. When the beam bends, the material along the top edge stretches while the material along the bottom compresses. This is seen by the fact that the new relative position, $$\delta {\vec r}_1$$, from orange to yellow is now shorter in length and has components in both directions (its original length and direction being shown in red). Likewise, the relative position between yellow and black changes its orientation substantially but negligibly changes its length since both points are along the edge and the bending stress barely compresses the material at the edge.

The deformation of the relative position from the orange and yellow points measures how much change $$\delta {\vec r}_0$$ suffers under the load of the bending stress. Care needs to be exercised when examining the change in orientation since a rigid body rotation does not constitute deformation even though it rotates the entire body. Thus, the measure of deformation should look something like

\[ deformation = \delta {\vec r}_1 – \delta {\vec r}_2 – rigid\;\;body\;\;rotations \; ,\]

with the additional understanding that this deformation will vary from point to point within the material, that is, the deformation is a field.

The mathematical characterization of deformation presented here closely follows Mathematical Methods for Physicists by Arfken, Third Edition.

Like the bending beam discussed above, Arfken focuses on two points at $${\mathcal P}_0$$ and $${\mathcal Q}_0$$.

Assume $${\mathcal P}_0$$ is located at $${\vec r}$$ and that the relative position of $${\mathcal Q}_0$$ is $$\delta {\vec r}$$. Under the applied stress, $${\mathcal P}_0$$ transports by $${\vec u}(\vec r)$$ to its new location at $${\mathcal P}_1$$. Likewise, $${\mathcal Q}_0$$ transports by $${\vec u}(\vec r + \delta {\vec r})$$ to its new location $$\delta {\vec r}’ = {\vec u} + \delta {\vec u}$$ relative to $${\mathcal P}_1$$. Because it describes the transport of each point in the material, $${\vec u}({\vec r})$$ is called the transport field.

Since a rigid-body motion would have transported both $${\mathcal P}_0$$ and $${\mathcal Q}_0$$ by a common $${\vec u}$$, independent of position, the deformation is clearly related to any transport difference, $$\delta {\vec u}$$, between the two.

The transport difference

\[ \delta {\vec u}({\vec r}) = {\vec u}({\vec r}+\delta {\vec r}) – {\vec u}({\vec r}) \; \]

expands, to first order, as

\[ \delta {\vec u} = \nabla_{\vec r} {\vec u} \cdot {\vec r} \; .\]

The gradient of the transport field is a second-rank tensor, called the transport tensor, that maps an initial relative position to a final transport difference. In components, its representation is

\[ \nabla {\vec u} = \frac{\partial u_i}{\partial r_j} \delta r_j \equiv \partial_j u_i \delta r_j \; . \]

It is important to realize that $$\nabla {\vec u}$$ is not yet the strain tensor being hunted. There is a possibility that there is a rotation hidden within.

The usual way to deal with this is to decompose the transport tensor into symmetric and anti-symmetric pieces defined through

\[ \delta u_i = \eta_{ij} \delta r_j + \xi_{ij} \delta r_j \; , \]

where

\[ \eta_{ij} = \frac{1}{2} \left( \partial_j u_i + \partial_i u_j \right) \, \]

and

\[ \xi_{ij} = \frac{1}{2} \left( \partial_j u_i – \partial_i u_j \right) \, . \]

Arfken notes that the anti-symmetric piece, which is related to the curl of the transport field, contains the rigid-body rotations. To see this, consider the following expression

\[ [ (\nabla \times {\vec u}) \times \delta {\vec r} ]_i = \epsilon_{ijk} \epsilon_{j\ell m} \partial_{\ell} u_m \delta r_k \; , \]

where $$[{\vec r}]_j \equiv r_j$$ is the jth component of the vector $${\vec r}$$.

Performing the usual index gymnastics yields
\[ [ (\nabla \times {\vec u}) \times \delta {\vec r} ]_i = \partial_j u_i \delta r_j – \partial_i u_j \delta r_j = 2 \xi_{ij} \delta r_j \; . \]

So the anti-symmetric portion of the transport difference represents a rotation of $${\mathcal Q}$$ about $${\mathcal P}$$ along the $$\nabla \times {\vec u}$$ axis by $$|\nabla \times {\vec u}|$$ radians.

The symmetric piece of the transport difference, $$\eta_{ij}$$, represents the actual strain that develops at $${\vec r}$$.

The diagonal components of $$\eta_{ij}$$ represent stretches or compressions and the off-diagonal components correspond to shears. To see these assertions consider the original orange and yellow points separated from each other by one unit of distance along the horizontal, which, for convenience, will be called the x-axis: ($$\delta {\vec x} = {\hat \imath} $$).

After the deformation, the transport difference is given by

\[ \delta {\vec u} = \eta_{11} {\hat \imath} + \eta_{12} {\hat \jmath} + \eta_{13} {\hat k} \; .\]

The position of yellow relative to orange is given by

\[ \delta {\vec y} = \delta {\vec x} + \delta {\vec u} = (1 + \eta_{11} ) {\hat \imath} + \eta_{12} {\hat \jmath} + \eta_{13} {\hat k} \; .\]

Projected into two dimensions, the before and after configurations look as below.

Note that the change in the relative position has components along both the $$x$$- and $$y$$-axes, with the later growing larger as the distance along the $$x$$-axes from the orange point grows. Since the length of the relative position changed, there is a scaling involved. Also, the growth along the $$x$$-axis of the vertical component represents a shear in contrast to a rotation.

With the basic notions of the strain tensor $$\eta_{ij}$$ well established, the next post will cover the mapping of this tensor to the various moduli of elasticity.

Up to this point in these posts on continuum mechanics, everything has been generally applicable.  The material derivative, the Reynolds and Flux transport theorems, and the nature of the stress tensor are applicable to any type of continuum.  Unfortunately, the party needs to end at some point and this post can be considered as the ‘last call’ that signals that end.

To understand why the generalities must stop, we need to discuss something mathematical and something physical.

On the mathematical side, we ultimately need to remind ourselves of a fact that is easy to lose sight of amidst all this machinery.  Namely, we are seeking to solve for the behavior of the continuum as a function of time.  We are seeking to generalize Newton’s laws to the continuum.

In their conventional setting, Newton’s laws amount to the following statement:

\[ m \frac{d^2 {\bar q}(t)}{d t^2} = {\bar f}({\bar q},{\dot {\bar q}},t) \; , \]

where $$\dot {\bar q}$$ stands for the time-derivative of $${\bar q}(t)$$ as a function of time.  The key point here is that the force on the right-hand side, $$\bar f$$ can be determined by knowing the current state itself (state being defined as the phase-space ordered pair of $$({\bar q},{\bar{\dot q}})$$ and time).  If this relationship didn’t exist, then literally there would be no way to evolve the system forward in time.  Some entity somewhere would need to supply the rule for how to compute the force at each step.

When generalized to a continuum setting, these underlying mathematical requires still hold sway but in a modified form.  To give some sense how this modified form might look, consider the wave equation,

\[ \frac{\partial^2 A(x,t)}{\partial t^2} = v^2 \frac{\partial^2 A(x,t)}{\partial x^2} \;, \]

as it is usually presented for the amplitude of a vibrating string $$A(x,t)$$.  This equation is usually derived in the continuum limit by looking at a small portion of the string and analyzing the tensions pulling on each side (see, e.g., Mechanics by Symon).  The right-hand side of the wave equation is the force on each infinitesimal length of string located at $$x$$.  To see this, note that another path to the wave equation uses a discrete, lumped-coupled mass-spring system.  This system is then transitioned into a continuum using the appropriate limit as the masses and the spacing between them both go to zero such that ratio of mass to spacing length goes to the mass density.  The article on the wave equation in Wikipedia, has an accessible presentation of this latter derivation using discrete masses and springs obeying Hooke’s law.

The point that is again worth emphasizing is that the force on the continuum is known in terms of the continuum itself.  Here the state of the system is characterized in terms of the spatial variation of $$A(x,t)$$ through its second partial derivative with respect to $$x$$.  This characterization looks odd at first glance but when expressed in terms of finite differences,

\[ \frac{\partial^2 A(x,t)}{\partial x^2} \approx \frac{A(x+h,t) – 2 A(x,t) + A(x-h,t)}{h^2} \; \]

it merely expresses the ‘force’ in terms of the state of the string at points $$x-h, x, x+h$$ and should be considered as no more odd than expressing the force as the combination

\[ \frac{\vec r}{\sqrt{x^2 + y^2 + z^2}} \; \]

as is done for central force laws.

Obviously, what we need to find for continuum mechanics is a relationship that specifies the stress in terms of some function of the state of the continuum.  We should prepare ourselves for the fact that the function will almost always depend on some spatial and, perhaps, temporal derivative.  We actually got a foretaste of that in the final result of the Reynolds transport theorem

\[ \frac{d}{dt} Vol(t) = Vol(t) div(\vec V) \; , \]

which relates the kinematic description of a small volume to the spatial variation of the flow velocity.

The final step is to sketch out the physical expectations for how that relationship might look functionally for various materials.  It is here that the fork in the road comes for which individual materials behave remarkedly different.

In the case of a simple elastic material, the body deforms with an application of a force but returns to its equilibrium shape with the removal of the load.  The picture looks something like this:

In continuum mechanics, the deformation of the material is described by comparing the initial configuration of the body (usually called the reference configuration) to the configuration after application of the load (usually called the current configuration).  The strain of the body (i.e. the response) finds expression in the relative movement of a set of points in the reference configuration to the same set in the current configuration.  Removing rigid-body motion leaves what is called the strain.  The outcome of this operation is to provide a direct functional connection $$\sigma = f(\epsilon)$$ between the observed strain, $$\epsilon$$, and the applied stress, $$\sigma$$, which is what is needed to have mathematical closure.   This relationship generalizes the usual Hooke’s law encountered in basic mechanics, which states that the force due to a spring is given by $$\vec F = -k \vec x$$, but the generalization, although still linear, is a bit more complicated due to tensorial nature of the stress and strain.

In contrast to elastic materials, whose deformation only persists as long as the stress is applied, fluids (liquids and gases) flow under the application of a stress.  Their deformations continue to change after the load is removed.

In these cases, the key observation comes from Newtonians laws.  The stress being an outside force, can only accelerate the material during its application.  The key relationship that relates the stress to an observed property of the body is of the form $$\sigma = f(\dot \epsilon)$$, which says that by observing the rate-of-change of the strain one can deduce the stress-applied.

To be complete, the two relationships detailed above only scratch the surface of the various types of materials and the resulting functional relationships between strain in a body and the stress applied.  There are hosts of other behaviors and often the situation is muddled due to the fact that the functional relationship is determined ‘the other way around’.  New materials are subjected to a variety of known stresses in order to observe the corresponding strains.  This approach results in an implicit relationship between strain and stress.  But regardless of whether the relationship is explicit or implicit, the mathematical closure of the theory requires that the force on the material be expressible as a function of the state of the material and, perhaps time, just as it is done for ordinary particle mechanics.

The coming posts will explore some of these relationships explicitly but no attempt to be complete and comprehensive will be made – nature is just too varied to believe that can be done.

 

The last set of posts have centered on describing the kinematics of continua by defining the material derivative and the Reynolds and Flux transport theorems. But kinematics by themselves are not much fun without being able to describe the forces that cause the kinematics. Forces within the realm of continuum mechanics are generally called stresses and the changes that they cause in the position and velocity of an element are called strains and strain rates.
The central player in determining a continuum’s dynamics is the stress tensor, which is a rank two tensor that takes in the position vector and the area times the normal to a surface in the continuum as inputs and returns the vector of force acting on that surface at that point. Pictorially, the situation looks like

while in abstract mathematical notation the tensor is described as

\[ \mathbf{T}(\vec r) \cdot d\vec S = \vec F \; , \]

where $$A$$ is the differential area of the face of the continuum (all of these results are exact in the limit as the size of the fluid element goes to zero).

There are two points worth discussing. First, it may not be at all obvious why the force should have components that do not lie along the surface normal. Second, assuming a satisfactory answer to the first question, why is the relationship between the force and the surface normal linear, as required for it to be a tensor relation.
The first question is the easier of the two to answer. Consider the surface force a block experiences as it rests upon a table top.

In this case, the normal force $$\vec N$$ lies anti-parallel to the unit normal $$\hat n$$ (note that the sign is matter of convention and different authors define a positive normal force to be when the force acts to compress the element, other authors when the force seeks to extend the element). Gravity plays no role here since it acts on each part of the body in the same way resulting in no stress (this fails to hold in a non-uniform field). The same situation would hold for a block sliding down a frictionless plane as the only stress on the surface of the block touching the incline plane is still normal to the surface.

However, the addition of friction ($${\vec F}_{f}$$) between the block and the plane creates a situation where the total force, $${\vec F}_{tot}$$, acting on the surface no longer lies along (either parallel or anti-parallel) to the surface normal. The component of force parallel to the interface between the block and the plane is a known as a shear force, with friction being the cause in this case.

If the angle of the incline plane is varied, the surface normal changes direction and the total force responds in kind, thus establishing the dependence on $$\hat n$$. If the roughness of the plane varies along its length, the direction and magnitude of $${\vec F}_{tot}$$ will also vary, thus establishing the dependence of the position vector $$\vec r$$. Properly interpreted, the concept of a force acting on a surface of a continuum that falls in a direction different from the surfaces unit normal and that has a spatial dependence can be found even in one of the most familiar scenarios from basic mechanics.

The response of a continuum to the application of a shear force is one of the primary ways in which matter is separated into its various phases (solid, liquid, gas, or plasma) and will the subject of future posts.

In order to answer why the mapping from surface normal to force should be linear, one must demonstrate the mapping is linear with respect to both scalar multiplication and vector addition as summarized in

\[ {\mathbf T} \cdot (c_1 d {\vec S}_1 + c_2 d {\vec S}_2 ) = c_1 {\mathbf T} \cdot d {\vec S}_1 + d {\mathbf T} \cdot d {\vec S_2} \; . \]

Symon covers this point nicely in Section 10.6 of his Mechanics (2nd edition) and I won’t bother to repeat the steps in detail. The key observation is that in shrinking the fluid element to zero, for example by multiplying by a small factor that Symon calls $$\alpha$$, the inertial side of Newton’s second law scales as $$\alpha^3$$, since it is proportional to density times volume, while the dynamic side of Newton’s second law scales as $$\alpha^2$$, since the force is proportional to the area. Symon then considers this scaling applied to a triangular prism where the normal to one face can be expressed in terms of the other two as $$d {\vec S}_3 = – d {\vec S}_1 – d {\vec S}_2$$. The only way to prevent a catastrophic build up in acceleration on the fluid element is if the sum the forces over all the faces is identically zero which can only happen if the mapping is linear (i.e. a tensor relationship).

There is one further point worth noting. The stress tensor $${\mathbf T}$$ must be a symmetric tensor; in index notation $$T_{ij} = T_{ji}$$. Thorne and Blandford show in Chapter 1 of Modern Classical Physics that the symmetry of the stress tensor follows by considering the effects of the torques (shear forces) on four sides of a cubical element with side length $$L$$. In their example, they determine the torque on the faces whose normals are parallel to the $$x$$-axis due to shears in the $$y$$-direction (i.e. $$T_{xy}$$) and find that the total torque is

\[ {\vec \tau}_z = T_{xy} L^3/2 \; .\]

Likewise, the torque on the faces whose normals are parallel to the $$y$$-axis due to shears in the $$x$$-direction has a total torque of

\[ {\vec \tau}_z = T_{yx} L^3/2 \; .\]

The sum of these torques has to equal to the time rate-of-change of the angular momentum, which gives

\[ (T_{xy} – T_{yx} ) L^3 = \frac{1}{6} \rho L^5 \frac{d L_z}{d t} \; .\]

Using a scaling argument similar to Symon’s one discussed above, one concludes that as $$L$$ goes to zero, the only physical way to prevent infinitely large angular accelerations is to have

\[ T_{xy} = T_{yx} \; .\]

This generalizes immediately to stress tensor as a whole being symmetric.

This analysis then completes the basic characterization of the stresses in a continuum. The next post will look at how materials respond to the application of the stresses.

This post completes the analysis of the transport theorems begun last month.  The Reynolds transport theorem, derived in the previous post, will be used to motivate the Flux transport theorem.  The result will then be generalized to account for a term that wasn’t captured in the first derivation.  On the surface, presenting two derivations of the Flux transport theorem may appear redundant but the derivation from the Reynolds theorem (including the explanation of the missing term) provides valuable insight into a very important point from differential geometry and provides a check for the more abstract derivation of the Flux transport theorem that follows.  The Flux transport theorem is important for a variety of reasons, not the least of which is that it underlies the Alfvén’s frozen in theorem, which led to the 1970 Nobel prize in physics.  As before, the derivations presented in this post draw heavily from Introduction to Vector Analysis, 4^th ed. By Davis and Snider.

Start with the density version of the Reynolds theorem that states

\[ \frac{d}{dt} \int d {\mathcal V}ol \; \rho = \int d {\mathcal V}ol \left( \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec V) \right) \; . \]

Ordinarily, the scalar function $$\rho$$ is the mass density, but for this derivation, it is better to think abstractly and to regard $$\rho$$ as the divergence of some vector field $$\vec F$$.  There always exists a Greens function (see an earlier post on the Helmholtz theorem) that specifies the vector field in terms of its divergence through the relation

\[ \vec F(\vec r) = \frac{1}{4\pi} \int d {\mathcal Vol} \; \frac{\rho(\vec r\;’) (\vec r – \vec r\;’)}{| \vec r – \vec r\;’|^3} \; . \]

The first step is to explicitly substitute

\[ \rho = \nabla \cdot \vec F \]

into the Reynold theorem to get

\[ \frac{d}{dt} \int d {\mathcal V}ol \; \nabla \cdot \vec F = \int d {\mathcal V}ol \; \frac{\partial}{\partial t} \nabla \cdot \vec F + \int d Vol \; \nabla \cdot \left( (\nabla \cdot \vec F) \vec V \right) \; .\]

Next, switch the order of integration in the first integral, which can always be done if the functions involved are smooth enough (a very modest requirement always met by physically realistic functions) to get

\[ \frac{d}{dt} \int d {\mathcal V}ol \; \nabla \cdot \vec F = \int d {\mathcal V}ol \; \nabla \cdot \left(\frac{\partial \vec F}{\partial t} \right) + \int d {\mathcal V}ol \; \nabla \cdot \left( (\nabla \cdot \vec F) \vec V \right) \; .\]

Applying the divergence theorem to all the integrals gives the Flux transport theorem (up to a missing term that is identically zero)

\[ \frac{d}{dt} \int d \vec S \cdot \vec F = \int d \vec S \cdot \left( \frac{\partial \vec F}{\partial t} + (\nabla \cdot \vec F) \vec V \right) \; .\]

As it stands, this derivation is exact for all closed volumes, $$\mathcal V$$, since closed volumes are bounded by closed surfaces, $$\mathcal S$$, (think of a ball bounded by a sphere).  The missing ‘zero’ term ‘corrects’ the theorem when the flux through an open surface, which possesses a bounding curve, is desired.  The realization that a closed surface, which is a boundary to some volume, lacks a boundary for itself is usually summarized by the phrase “the boundary of a boundary is zero”, which is attributed to John Wheeler.  This latter point is of central importance to differential geometry and general relativity.

To account for this missing term, we now turn to a more complete derivation of the Flux transport theorem.  Imagine an open surface, $${\mathcal S}_t$$, bounded by the curve $${\mathcal C}_t$$, that is transported by a flow from time $$t_1$$ to $$t_2 = t_1 + \Delta t$$, during which its location, size, and shape change.  These changes are represented by differences in the surface normals $$\hat n_1$$ and $$\hat n_2$$ and in the bounding curves $${\mathcal C}_1$$ and $${\mathcal C}_2$$ and the corresponding tangent vectors $$\hat t_1$$ and $$\hat t_2$$.

Like a single particle’s trajectory can be thought to trace a path through space, this surface, being two-dimensional, can be thought to trace out a volume, $${\mathcal V}_{total}$$.  It is important to remember that to identify the surface’s motion with the volume it crosses, several important changes have to be considered.

First the surface normal on the ‘bottom’ surface must be reversed so that it correspond to the outward normal

\[ \hat n_1 \rightarrow – \hat n_1 \; \]

and that the vector field whose flux is piercing this surface must be evaluated at a common time, which can be arbitrarily chose, without loss of generality, to be $$t_1$$.

In doing so, the time-varying flux integral has been changed to a volume integral over $${\mathcal V}_{total}$$ at a common time, and the application of the divergence theorem can be used.

The details are as follows.  The integral of $$\vec F$$ over the closed surface, $${\mathcal S}_{total}$$ bounding this volume is made of three pieces

\[ \oint_{{\mathcal S}_{total}} d \vec S \cdot \vec F = \int_{top} d \vec S \cdot \vec F + \int_{bottom} d \vec S \cdot \vec F + \int_{side} d \vec S \cdot \vec F \; .\]

The integral over the top surface can be related to the integral over the corresponding surface at time $$t_2$$ by means of the Taylor expansion

\[ \vec F(\vec r, t_2) = \vec F(\vec r, t_1) + \frac{\partial \vec F}{\partial t}(\vec r, t_1) \Delta t + \cdots \; \]

to get

\[ \int_{top} d \vec S \cdot \vec F = \int_{top} d \vec S \cdot \left( \vec F – \frac{\partial \vec F}{\partial t} \Delta t \right) = \int_{{\mathcal S}_2} d \vec S \cdot \left( \vec F – \frac{\partial \vec F}{\partial t} \Delta t \right) \; .\]

The integral over the bottom surface can be related to the integral over the corresponding surface at time $$t_1$$ by means of an overall minus sign reflecting the difference between the volume outward normal and the surface normal

\[ \int_{bottom} d \vec S \cdot \vec F = – \int_{{\mathcal S}_1} d \vec S \cdot \vec F \; .\]

The last piece is the integral over the side.  The surface element of the side is

\[ d \vec S_{side} = d\ell \, \hat t \times \vec V \Delta t \; ,\]

where $$\hat t$$ is oriented tangent to $${\mathcal C}_1$$ and $$d \ell$$ is the differential length along it, since this gives the surface area of the parallelogram multiplied by the outward surface normal.  The resulting integral is then

\[ \int_{side} d \vec S \cdot \vec F = \int_{{\mathcal C}_1} (d\ell \, \hat t \times \vec V \Delta t) \cdot \vec F = – \int_{side} d\ell \, \hat t \cdot (\vec F \times \vec V \Delta t) \; , \]

where the commutative property of the triple-scalar product was used in the last term.

By the divergence theorem,

\[ \oint_{{\mathcal S}_{total}} d \vec S \cdot \vec F = \int_{{\mathcal V}_{total}} d {\mathcal V}ol \; \nabla \cdot \vec F \; .\]

This latter integral can be further simplified by noting that the volume of any ‘tube’ making up the volume is the area of the base $$d \vec S$$ times (via the scalar product) the height $$\vec V \Delta t$$, giving

\[ d {\mathcal V}ol = d \vec S \cdot \vec V \Delta t \; ,\]

where the surface element is understood to point along $$\hat n_1$$.

The final form of the recast total surface integral is then

\[ \oint_{{\mathcal S}_{total}} d \vec S \cdot \vec F = \int_{{\mathcal S}_{1}} d \vec S \cdot \left( (\nabla \cdot \vec F) \vec V \right) \Delta t \; .\]

Putting the pieces together gives

\[ \int_{{\mathcal S}_{1}} d \vec S \cdot \left( (\nabla \cdot \vec F) \vec V \right) \Delta t = \int_{{\mathcal S}_2} d \vec S \cdot \left( \vec F – \frac{\partial \vec F}{\partial t} \Delta t \right) \\ – \int_{{\mathcal S}_1} d \vec S \cdot \vec F – \int_{{\mathcal C}_1} d\ell \, \hat t \cdot (\vec F \times \vec V \Delta t) \; , \]

where $$\vec F$$ is evaluated at time $$t_1$$ in every term but the first part of the first term on the right-hand side.

Re-arranging the terms results in

\[ \int_{{\mathcal S}_2} d \vec S \cdot \vec F – \int_{{\mathcal S}_1} d \vec S \cdot \vec F = \int_{{\mathcal S}_2} d \vec S \cdot \frac{\partial \vec F}{\partial t} \Delta t \\ + \int_{{\mathcal S}_1} d \vec S \cdot \vec V (\nabla \cdot \vec F) \Delta t + \int_{{\mathcal C}_1} d\ell \, \hat t \cdot (\vec F \times \vec V) \Delta t \; .\]

Dividing the left-hand side by $$\Delta t$$ and taking the limit gives

\[ \lim_{\Delta t \rightarrow 0} \frac{1}{\Delta t} \left( \int_{{\mathcal S}_2} d \vec S \cdot \vec F – \int_{{\mathcal S}_1} d \vec S \cdot \vec F \right) = \frac{d}{dt} \int_{{\mathcal S}_1} d \vec S \cdot \vec F \equiv \frac{d}{dt} \Phi_{\vec F} \; , \]

which is exactly the time derivative of the flux $$\Phi_{\vec F}$$ of $$\vec F$$ through the surface.  Thus

\[ \frac{d}{dt} \Phi_{\vec F} = \int_{{\mathcal S}_1} d \vec S \cdot \left( \frac{\partial \vec F}{\partial t} + \vec V (\nabla \cdot \vec F) \right) + \int_{{\mathcal C}_1} d\ell \, \hat t \cdot (\vec F \times \vec V) \; ,\]

where in the limit $${\mathcal S}_2$$ becomes $${\mathcal S}_1$$.

The final step involves recalling that $$t_1$$ was an arbitrary time and so the ‘1’ can be dropped to give

\[ \frac{d}{dt} \Phi_{\vec F} = \int_{{\mathcal S}_t} d \vec S \cdot \left( \frac{\partial \vec F}{\partial t} + \vec V (\nabla \cdot \vec F) \right) + \oint_{{\mathcal C}_t} d\ell \, \hat t \cdot (\vec F \times \vec V) \; .\]

which is the Flux transport theorem in all its glory.