This installment was intended to be a realigning of the recent series of articles on continuum mechanics to a set of columns specialized to fluid mechanics. However, there is a nice derivation of the inner workings of the stress tensor that I developed while working on the new post on fluids that is worthy of some daylight. In some sense, this post (and the one that follows) adds the rigor that was missing from the general discussion presented in the column entitled Continuum Mechanics 5 – The Stress Tensor. So, this month’s offering is a complete rederivation of a coordinate-free representation of the stress tensor.
As discussed in that earlier post, the force on a surface is naturally a function of the surface normal. What was taken on authority was that the mapping should be linear (i.e., tensorial) and symmetric in order that there be no unphysical translational and angular accelerations, respectively. This post will prove that the mapping should be linear, and next month’s post will provide a rigorous derivation of the symmetry properties.
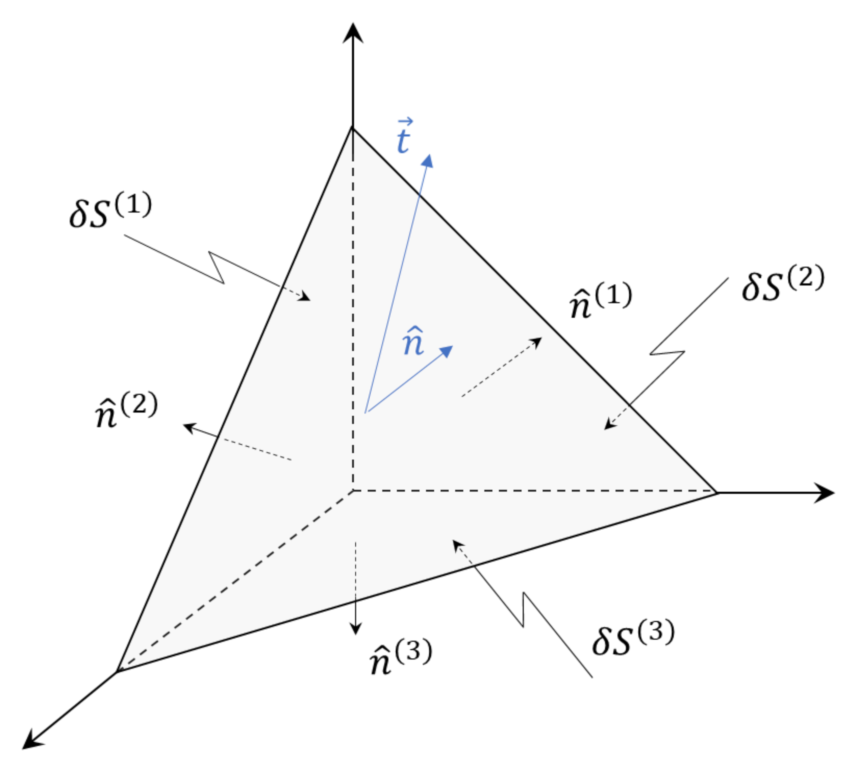
All that is needed to construct a mathematical derivation are some basic physical principles and elementary mathematics. The starting point for the derivation is Cauchy’s tetrahedron,
a portion of the continuum where three sides of the figure (denoted by the superscripts $$(1), (2), (3)$$) coincide with coordinate planes (i.e., $$x$$-$$y$$, $$y$$-$$z$$, and $$z$$-$$x$$ planes) and the fourth side (no superscript) closes the shape.
The physical principles that we will employ are Newton’s laws, the fact that the surface force across an interface is proportional to the area of the interface, and the fact that the volume scales as the cube of some characteristic length $$L$$ while the area scales as the square.
Newton’s second law applied to the tetrahedron yields
\[ m_{T} \, {\vec a}_{T} = {\vec f}^{(1)} + {\vec f}^{(2)} + {\vec f}^{(3)} + {\vec f} \equiv {\vec f}_{total} \; ,\]
where $$m_{T}$$ is the mass of the tetrahedron and $${\vec a}_{T}$$ is the acceleration. Since the mass of the tetrahedron is the product of the mass density times the volume, $$\rho {\mathcal V}_T$$, it scales as $$\alpha^3$$ as each linear dimension is scaled by a factor $$\alpha$$. Each of the forces on the right-hand side is proportional to an area of the face (e.g., $${\vec f}^{(1)} \propto \delta S^{(1)}$$), it scales as $$\alpha^2$$ as each linear dimension is scaled by the same factor $$\alpha$$.
The entire equation, when subjected to this scaling, becomes
\[ m_{\mathcal T} \, \alpha^3 \, {\vec a}_{T} = \alpha^2 {\vec f}_{total} \; .\]
Dividing through by $$\alpha$$, gives the acceleration as
\[ {\vec a}_{T} = \frac{1}{\alpha \, m_{T}} {\vec f}_{total} \; .\]
In order to prevent an infinite acceleration as $$\alpha \rightarrow 0$$, we require that the forces exactly balance to zero.
\[ {\vec f}_{total} = {\vec f}^{(1)} + {\vec f}^{(2)} + {\vec f}^{(3)} + {\vec f} = 0 \; .\]
Now we want to characterize the forces. Since we know that each force is proportional to the area and depends on the normal we can write the mapping generally as
\[ {\vec f}^{(i)} = {\mathbf T}\left({\hat n}^{(i)}\right) \delta S^{(i)} \; , \]
for $$i = 1, 2, 3$$ and ‘blank’ (that is, no superscript for the oblique face).
From Newton’s third law, we know that the force on one side of an interface must be equal and opposite to the force on the other side. This relationship requires that
\[ {\mathbf T}({\hat n}) = – {\mathbf T}({\hat n}) \; . \]
By their orientation, the faces that coincide with a coordinate plane have unit normals that relate to the basis vectors as
\[ {\hat n}_1 = – {\hat e}_1 \; , \]
\[ {\hat n}_2 = – {\hat e}_2 \; , \]
and
\[ {\hat n}_3 = – {\hat e}_3 \; . \]
From basic geometry, the areas of each of these planes are related to the area of the fourth plane by
\[ \delta S_1 = {\hat n} \cdot {\hat e}_x \, \delta S \; , \]
\[ \delta S_2 = {\hat n} \cdot {\hat e}_y \, \delta S \; , \]
and
\[ \delta S_3 = {\hat n} \cdot {\hat e}_z \, \delta S \; . \]
Since the set $$\{{\hat e}_x, {\hat e}_x, {\hat e}_x,\}$$ spans the space, the normal to the oblique face can be decomposed as
\[ {\hat n} = ({\hat e}_x \cdot {\hat n}) {\hat e}_x + ({\hat e}_y \cdot {\hat n}) {\hat e}_y + ({\hat e}_z \cdot {\hat n}) {\hat e}_z \equiv a \, {\hat e}_x + b \, {\hat e}_y + c \, {\hat e}_z \; . \]
Returning to the force equilibrium, and expressing the forces in terms of the stress and areas, and the areas of the faces aligned with the coordinate planes in terms of the area of the oblique face, yields
\[ {\mathbf T}({\hat n}) \, \delta S = – {\mathbf T} \left( {\hat n}^{(1)} \right) \, ({\hat e}_x \cdot {\hat n} ) \, \delta S \\ – {\mathbf T} \left( {\hat n}^{(2)} \right) ({\hat e}_y \cdot {\hat n} ) \, \delta S \\ – {\mathbf T} \left({\hat n}^{(3)} \right) ({\hat e}_z \cdot {\hat n} ) \, \delta S \; . \]
Divide out the common factor of $$\delta S$$, replace the dot products of the normal with the basic vectors by the components, and exploit Newton’s third law to absorb the minus signs on the right-hand side
\[ {\mathbf T}({\hat n}) = a {\mathbf T} \left({\hat e}_{x}\right) + b {\mathbf T} \left({\hat e}_{y}\right) + c {\mathbf T} \left({\hat e}_{z}\right) \; . \]
Finally, substitute in the form of the normal into the left-hand side to get
\[ {\mathbf T}\left( a {\hat e}_x + b {\hat e}_y + c {\hat e}_z \right) = a {\mathbf T} \left({\hat e}_{x}\right) + b {\mathbf T} \left({\hat e}_{y}\right) + c {\mathbf T} \left({\hat e}_{z}\right) \; . \]
The foregoing result is the definition of a tensorial relationship, and the first half of the proof is complete.