Last month’s column introduced the notion of the thermodynamic square as a mnemonic for organizing certain second-order partial derivatives amongst the various thermodynamic potentials: the internal energy $$U$$, the Gibbs and Helmholtz free energies $$G$$ and $$F$$, and the enthalpy $$H$$. As previously alluded to, physicist primarily use these relations (called the Maxwell Relations) to eliminate the terms difficult or impossible to measure experimentally in favor of parameters that are easily measured in the lab.
A practical example of the application of the Maxwell relations is the simplification of the ‘first’ and ‘second $$T dS$$ equations’ as listed in Exercise 7.3-1 on page 189 of Herbert B. Callen’s book Thermodynamics and an Introduction to Thermostatistics, 2nd edition. The relevant physical properties in these equations are (Sec. 3.9 of Callen):
- the number of particles $$N$$,
- the differential heat $$dQ = T dS$$,
- the heat capacity at constant volume $$c_V = \frac{T}{N} \left( \frac{\partial S }{\partial T} \right)_V= \frac{1}{N} \left(\frac{\partial Q }{\partial T}\right)_{V}$$,
- the heat capacity at constant pressure $$c_P = \frac{T}{N} \left( \frac{\partial S }{\partial T} \right)_P = \frac{1}{N}\left(\frac{\partial Q}{\partial T}\right)_{P}$$,
- the coefficient of thermal expansion $$\alpha = \frac{1}{V} \left(\frac{\partial V}{\partial T}\right)_P $$, and
- the isothermal compressibility $$\kappa_T = – \frac{1}{V} \left( \frac{\partial V}{\partial P} \right)_T$$.
First $$TdS$$ Relation
The first relation we want to verify is
\[ T dS = N c_V dT + \frac{T \alpha}{\kappa_T} dV \; .\]
From the form of this equation, assume that the quantity in question is the entropy as a function of the temperature and volume $$S = S(T,V)$$. Taking the first differential gives
\[ dS = \left(\frac{\partial S}{\partial T}\right)_{V} dT + \left(\frac{\partial S}{\partial V}\right)_{T} dV \; .\]
The first term is relatively easy to deal with in terms of the heat capacity at constant volume $$c_V$$:
\[ \left(\frac{\partial S}{\partial T}\right)_{V} = \frac{N c_V}{T} \; .\]
The second term requires a bit more work. First use the Maxwell relation associated with the Helmholtz free energy $$F$$
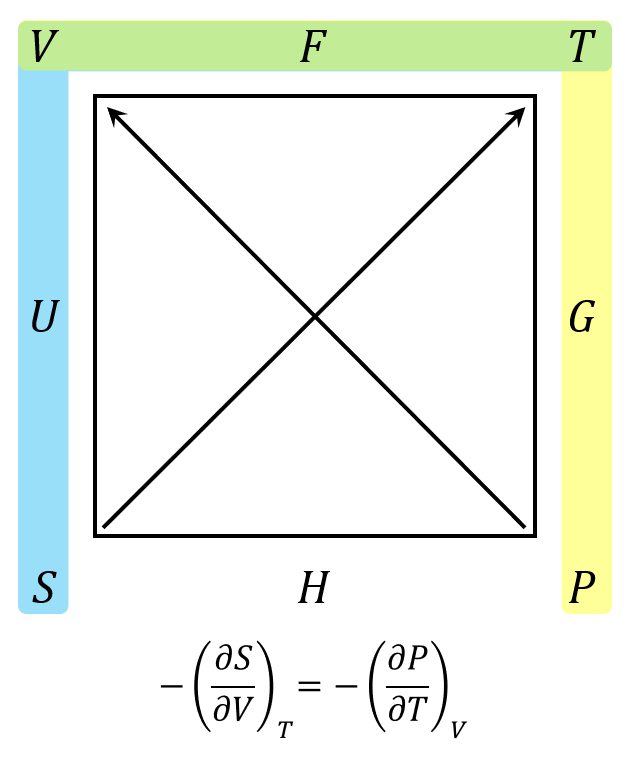
to get
\[ – \left(\frac{\partial S}{\partial V}\right)_{T} = – \left(\frac{\partial P}{\partial T}\right)_{V} \; .\]
Next use the second classical partial derivative identity
\[ \left(\frac{\partial P}{\partial T}\right)_{V} \left(\frac{\partial T}{\partial V}\right)_{P} \left(\frac{\partial V}{\partial P}\right)_{T} = – 1 \; ,\]
and solve for
\[ \left(\frac{\partial P}{\partial T}\right)_{V} = \frac{-1}{\left(\frac{\partial V}{\partial P}\right)_{T} \left(\frac{\partial T}{\partial V}\right)_{P} } \; . \]
Use another of the classical partial derivative identities to move the $$\left(\frac{\partial T}{\partial V}\right)_{P}$$ to the numerator to get
\[ \left(\frac{\partial P}{\partial V}\right)_{T} = – \left(\frac{\partial V}{\partial T}\right)_{P} / \left(\frac{\partial V}{\partial P}\right)_{T} \; .\]
Multiply the numerator and denominator by $$1/V$$ and use the definitions of $$\alpha$$ and $$\kappa_T$$ to get
\[ \left(\frac{\partial P}{\partial V}\right)_{T} = \frac{\alpha}{\kappa_T} \; . \]
At this point, the first differential stands as
\[ dS = \frac{N c_V}{T} dT + \frac{\alpha}{\kappa_T} dV \; . \]
Multiplying each side by $$T$$ gets us to the final form of the first $$T dS$$ equation
\[ T dS = N c_V dT + \left(\frac{T \alpha}{\kappa_T} \right) dV \; .\]
Second $$TdS$$ Relation
The second relation is
\[ T dS = N c_P dT – T V \alpha dP \; . \]
From the form of this equation, assume that the quantity in question is the entropy as a function of the temperature and pressure $$S = S(T,P)$$. As in the first $$T dS$$ relation, taking the first differential gives
\[ dS = \left(\frac{\partial S}{\partial T}\right)_{P} dT + \left(\frac{\partial S}{\partial P}\right)_{T} dV \; .\]
The first term, as in the case above, is also relatively easy to deal with in terms of the heat capacity, this time at constant volume, $$c_P$$:
\[ \left(\frac{\partial S}{\partial T}\right)_{P} = \frac{N c_P}{T} \; .\]
The second term only requires a Maxwell relation in terms of the Gibbs free energy
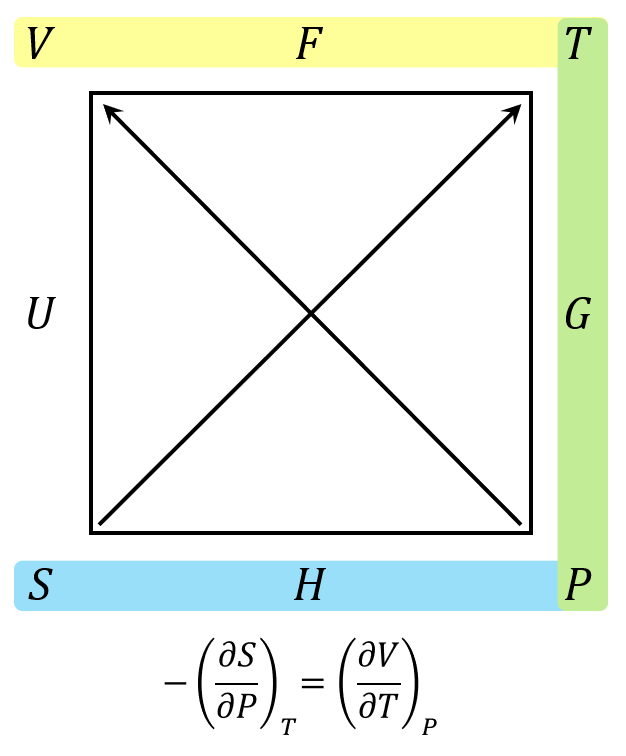
\[ -\left(\frac{\partial S}{\partial P}\right)_{T} = \left(\frac{\partial V}{\partial T}\right)_{P} \; .\]
The first differential becomes
\[ dS = \frac{N c_P}{T} dT – \left(\frac{\partial V}{\partial T}\right)_{P} dP \; .\]
Multiplying the second term by $$V/V$$ and simplifying gives
\[ dS = \frac{N c_P}{T} dT – V \alpha dP \; ,\]
which becomes the desired relation when multiplying both sides by $$T$$
\[ T dS = N c_P dT – T V \alpha dP \; .\]
To summarize, these two relations show how to express the heat $$T dS$$, expressed in terms of the entropy (which cannot be measured) in terms of parameters, such as temperature, pressure, and heat capacity, that are easily measured in the lab. All that is needed is the machinery of partial derivatives. This observation is the reason that so many textbooks on Thermodynamics have specific sections devoted to these approaches.
