One of the most difficult concepts I’ve ever encountered is the scattering cross section. The reason for this difficulty is not in its basic application but the fact that it there are so many of them, each tending to show up in different guises with slightly different definitions, each tailored to fit the particular circumstances. Being something of a generalist, I like to see the one, encompassing definition first and then adapt that definition to the problem at hand. Many and scattered (no pun intended) aspects of that central definition just makes my program much harder to fulfill.
It should come as no surprise that concepts surrounding physical scattering should be numerous and diverse. Scattering (or collision) between one object and another is a basic process that reflects the underlying truth that matter is competitive. No two objects (leaving bosons aside) can occupy the same space at the same time. Scattering is as ubiquitous as rotations and vibrations, without having the decency or charm to be confined to limited section of space.
Several aspects associated with the scattering cross section make it especially slippery. Collisions between objects can be quite complicated based on structure and regime. Extended or complex objects are particular hard to model and the complications associated with the transition from a classical regime to a quantum one adds layers of complexity.
So, for many years, the general notion of the scattering cross section remained elusive. Recently I’ve come back to the description presented in Physics by Halliday and Resnick. Since it was originally couched more within the context of elementary particle physics its applicability to other aspects of scattering was unclear. I’ll discuss below why I believe a generalization of it to be the best definition available, even for classical systems. But for now, lets talk about the physical model.
The Halliday and Resnick model is based on the scattering of elementary particles from a thin foil. They liken the scenario to firing a machine gun at a distant wall of area $$A$$. A host of small plates, $$N$$ of them in number, and each of area $$\sigma$$, are arranged on the wall without overlapping. If the rate at which the machine gun fires is $$I_0$$ and the it uniformly sprays bullets over the wall, then the fractional rate $$I$$ (fraction per unit time) that will impact a plate is given by
\[ \frac{I}{I_0} = \frac{N \sigma}{A} \equiv \frac{A_p}{A} \; ,\]
which is interpreted as the ratio of the total area covered by the plates $$A_p = N \sigma$$ to the total area of the wall.
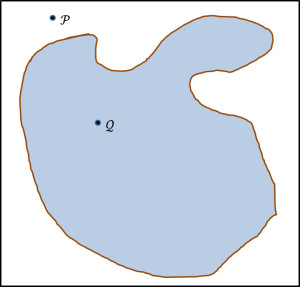
At its heart, this explanation is essentially the classic scenario for Monte Carlo analysis in which the area of an irregular shape (say a lake), $$A_I$$, is estimated by surrounding it with a regular shape (say a square plot of land) of known area, $$A_R$$.
The point $${\mathcal P}$$, which falls within $$A_R$$ but outside $$A_I$$ is termed a ‘miss’. The point $${\mathcal Q}$$, which falls within $$A_I$$ is termed a ‘hit’. By distributing points uniformly within $$A_R$$ and counting the ratio of hits, $$N_h$$, to total points used, $$N$$, the area of the irregular shape can be estimated as
\[ \frac{A_I}{A_R} = \frac{N_h}{N} \; ,\]
where the estimate becomes exact as $$N$$ tends to infinity.
The only difference with the classic Monte Carlo problem and the thin foil problem is that the irregular shape in the foil scenario is built out of many non-contiguous pieces.
Halliday and Resnick then generalize this definition by separating the universe of outcomes into more than two choices – hit or miss. They basically subdivide the hit space into additional outcomes like ‘hit the plate and break it into 3 pieces’ or ‘hit the plate and break it into 5 pieces’, and so on. Each of these outcomes can have their respective scattering cross sections given by
\[ \sigma_3 = \frac{A}{N} \frac{I_3}{I_0} \]
for the former case and
\[ \sigma_5 = \frac{A}{N} \frac{I_5}{I_0} \]
for the latter. Note that the factor $$\frac{A}{N}$$ lends units of area to the cross section, but otherwise just comes along for the ride.
An additional generalization to nuclear and particle physics occurs when the universe of possibilities is expanded to account number of particles scattered into a particular direction or to distinguish encounter when the species changes.
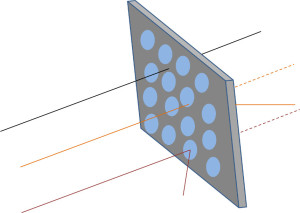
For scattering direction, the scenario looks something like
where the black trajectory is not scattered, the orange by a little, and the maroon by a lot.
For the case where the species changes, there can be dramatic differences like those listed in Modern Physics by Kenneth Krane. He asks the reader to consider the cross section for the following reactions involving certain isotopes of iodine and xenon:
\[ \begin{array}{lr} I + n \rightarrow I + n & \sigma = 4 b \\ Xe + n \rightarrow Xe + n & \sigma = 4 b \\ I + n \rightarrow I + \gamma & \sigma = 7 b\\ Xe + n \rightarrow Xe + \gamma & \sigma = 10^6 b \end{array} \; . \]
The first two reactions are inelastic scattering, the last two are neutron capture, and the units on cross section are in barns $$b= 10^{-28} m^2$$.
Now I appreciate that nuclear physicists like to work from the thin foil picture, and that, as a result, the definitions of cross section inherit the units from the geometric factor $$A/N$$ out in front. But in reality, their thinking isn’t really consistent with that. In the iodine and xenon example, the absolute values of cross sections are unimportant. What matters is that the likelihood that iodine and xenon will inelastically scatter a neutron are the same while the likelihood of these two elements capturing a neutron are 5 orders of magnitude different, with xenon a 100,000-times more likely.
So why bother assigning cross sections units of area. More physics would be unified if traditional cross sections derived in the above fashion were consistently reinterpreted to be Monte Carlo ratios. This improvement in thinking would unite classical and quantum concepts and would accommodate both deterministic and stochastic systems (regardless of the origin of the randomness). It would also remove that pedagogical thorn of the total scattering cross section of the $$1/r$$ potential as being infinite (which is hard to swallow and makes the cross section seem dodgy when learning it). The question simply no longer holds any meaning. The new interpretation would be that the ratio of particles scattered in any fashion relative to the number sent into the $$1/r$$ scatterer is exactly $$1$$ – i.e. every particle scatters a little. That is the essence of the ‘explanation’ of the infinite cross section (even in classical physics). There would be no area and thus no infinite area as well. It would also put $$1d$$ scattering off of step potentials on the same footing as $$3d$$ scattering. The transmission and reflection coefficients $$T$$ and $$R$$ now would have the same meaning as the scattering cross section. No superfilous and distracting units would separate one from the other.
Unfortunately, I doubt that the physics community would ever actually give up on nearly a century of data, but one can dream.