This week’s column is the last installment of a long and detailed look at scattering in classical mechanics. Up to this point specific potentials ($$1/r$$ and $$e^{-r/R}/r$$) have been used and the specific relationship between the impact parameter $$b$$ and the scattering angle $$\theta$$ has been derived either analytically ($$1/r$$) or numerically ($$1/r$$ and $$e^{-r/R}/r$$). This week, I am going to talk about scattering in general and clear up a few loose ends, including a close look at the traditional definition of scattering cross section.
One might argue that the omission of the scattering cross section in these previous studies has been glaring. But as I’ve argued elsewhere, I prefer the definition of the scattering cross section in terms of relative probability and I believe that the insistence on deriving ‘an effective area’ to be a hold over from the pre-quantum days when Rutherford scattering was a new technique and its results were revolutionary. While it is true that scattering results in particle physics still are expressed in barns (or some faction therein), their interpretation is clearly couched in terms of fractions of outcome events compared to all the possible events. In addition, in all my professional work in planetary flybys, I’ve never seen anyone actually calculate a scattering cross section. Rather everything is expressed in terms of impact parameter $$b$$ (from which the b-plane derives its name) and the bend or scattering angle. Even when performing Monte Carlo analysis of flyby control and navigation, no one suggests using cross section. Nonetheless, a really thorough treatment would be incomplete without some discussion.
My treatment here closely follows the arguments found in Chapter 6 of Introduction to Elementary Particles, 2nd edition by David Griffiths. Griffiths doesn’t present anything new, per se, but he is careful in his pedagogy – particularly his ‘derivation’ of $$\frac{d\sigma}{d\Omega}$$ and it is worth extending his approach.
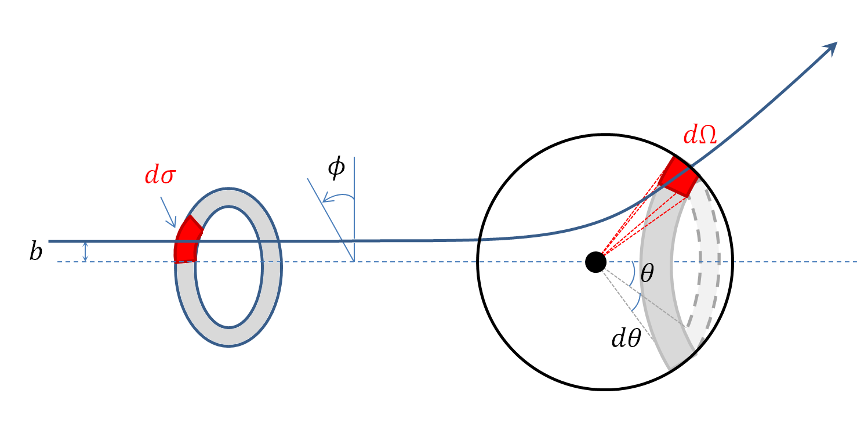
The generic scattering scenario is shown in the figure below.
In it, we imagine a uniform and collimated beam of particles streaming towards a scattering center. Focus on one slice through the beam at a point where the particles are still far from the scatterer. Narrow the focus again to those particles in an annular ring with inner radius $$b$$ and outer radius $$b+db$$, denoted by the gray shading. And, finally, narrow the focus one more time to particles in that ring that reside in the sector between azimuth angles $$\phi$$ and $$\phi + d\phi$$. This sector, of area $$d\sigma$$, is denoted by the red shading. As the annular ring propagates towards the scatter, the individual particles begin to be deflected and eventually, when sufficiently long time has passed, the ring will have become distorted into the gray annulus on the sphere surrounding the scatter. In particular, the original red sector has been transformed into a region of solid angle $$d\Omega$$ on the sphere. The (differential) scattering cross section relates the two through
\[ d \sigma = D(\theta,\phi) d \Omega \; .\]
The introduction of $$D(\theta, \phi)$$ by Griffiths is a nice pedagogical touch as it divorces the concept from the stupid notation $$\frac{d\sigma}{d\theta}$$ which is neither explanatory nor actually a derivative in the rigorous sense. By dimensional arguments, $$D(\theta,\phi)$$ must have units of area, a point on which I will elaborate more below.
The area of the sector is
\[ d\sigma = |b \, db \, d\phi| \]
and the solid angle is
\[ d\Omega = |\sin \theta \, d\theta \, d\phi| \; .\]
Note that since area and solid angle are intrinsically positive quantities, whereas $$db$$, $$d\phi$$, and $$d\theta$$ can have any sign, absolute value must be used.
Substituting these relations in and solving for $$D(\theta,\phi)$$ yields
\[ D(\theta,\phi) = \frac{d\sigma}{d\theta} = \frac{|b \, db \, d\phi|}{|\sin \theta \, d\theta \, d\phi|} = \frac{b}{\sin \theta}\left|\frac{db}{d\theta}\right| \; , \]
where $$b$$ and $$\sin\theta$$ can be taken out of the absolute values since they are always positive (since $$b$$ is a radius and $$\sin\theta \ge 0 $$ for $$\theta \in [0,\pi]$$).
So having the relationship between the impact parameter $$b$$ and the scattering angle $$\theta$$ is essentially the same as having the scattering cross section.
For the case of Coloumb scattering, the relationship (as derived in Part 3) is
\[ \cot^2 \left(\frac{\theta}{2}\right) = \frac{4 E^2 b^2}{\alpha^2} \; .\]
To get the scattering cross section, first solve for $$b$$ in terms of $$\theta$$ (note that since we will be taking an absolute value, the sign from the square root doesn’t matter)
\[ b = \frac{\alpha}{2 E} \cot \left( \frac{\theta}{2} \right) \]
and then take the derivative
\[ \left| \frac{db}{d\theta} \right| = \frac{\alpha}{4 E} \csc^2 \left( \frac{\theta}{2} \right) \; . \]
A clever rewriting of $$\sin \theta = 2 \sin\left(\frac{\theta}{2}\right) \cos\left(\frac{\theta}{2}\right)$$ gives
\[ D(\theta,\phi) = \frac{\frac{\alpha}{2E} \frac{\cos\left(\frac{\theta}{2}\right)}{\sin\left(\frac{\theta}{2}\right)}}{2 \sin\left(\frac{\theta}{2}\right) \cos\left(\frac{\theta}{2}\right)} \cdot \frac{\alpha}{4 E} \frac{1}{\sin^2\left(\frac{\theta}{2}\right)} = \; \; \; \frac{1}{4} \left(\frac{\alpha}{2E}\right)^2 \csc^4 \left( \frac{\theta}{2} \right) \; ,\]
which is the famous Rutherford result.
Physically, from the defining equation, $$D(\theta,\phi) d\Omega$$ is the area of the image of the incoming red sector under the action of the scattering. It is often expressed as
\[ D(\theta,\phi) d\Omega = \frac{\textrm{# of particles per unit time scattered into } d \Omega}{\textrm{incident intensity}} \; . \]
To see why, suppose that the incident intensity $$I_0$$ is given by
\[ I_0 = \frac{N}{A \delta t} \; ,\]
where $$N$$ is the number of particles in the beam, $$A$$ is the cross sectional area of the beam, and $$\delta t$$ is some measure of unit time. Let $$N_{d\Omega}$$ be the number of particles scattered in solid angle $$d\Omega$$. The unit of time cancels leaving
\[ D(\theta,\phi) d\Omega = A \frac{N_{d\Omega}}{N} \; ; \]
so, like in the Monte Carlo case discussed earlier, the area of the image can be inferred by counting how many particles end up in it relative to the number of particles sent in and multiplying the initial area of the beam by this scale factor. For those needing a bit more convincing, realize that the number of scattered particles $$N_{d\Omega}$$ is equal to the number of particles in the original red sector (this is a classical setting to local neighborhoods propagate into local neighborhoods). The number of particles in the original red sector is the fraction of cross sectional area it consumes times the total number or
\[ N_{d\Omega} = N_{d\sigma} = N \frac{d\sigma}{A} \; ,\]
which when substituted into the previous equation gives $$D(\theta,\phi) d \Omega = d\sigma$$ as desired. The experimentalist is likely to massage these last relationship into a pithier statement: $$D(\theta,\phi) d\Omega = N_{d\Omega} / I_0$$ (the cross section equals the particles counted divided by the beam intensity).
Nowhere in any of the above discussion is there an interpretation that says that $$D(\theta,\phi) d\Omega$$ is somehow the size of the scatterer. In fact, if one defines, the size of the scatter as
\[ S = \int d\Omega D(\theta,\phi) \]
then one is baffled by the result that, for Coloumb scattering, the size of the scatterer is infinite. Bigger than the experiment, bigger than the universe, and certainly so big as to thwart every assumption we have about incoming and outgoing unbound states. This is the heart of my objection to that interpretation.
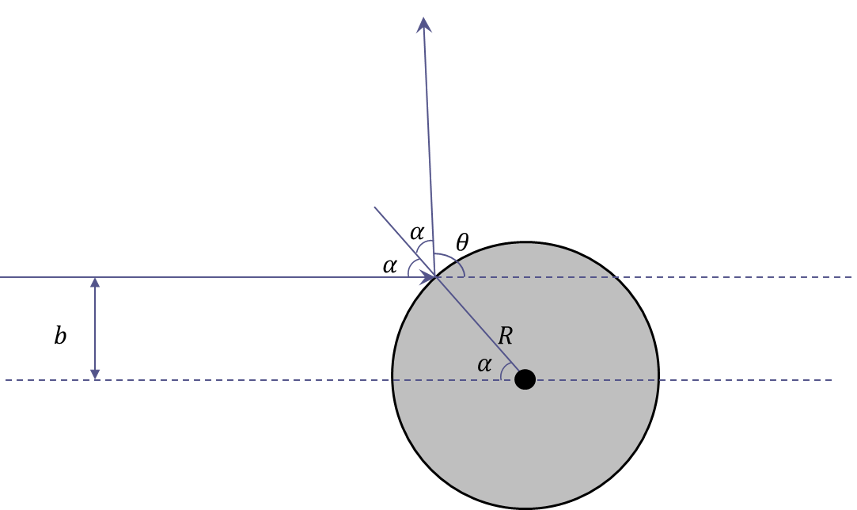
So from where does such an interpretation spring? Well, in one particular case – and only in this case – does it make some kind of sense. For scattering from a hard sphere
the relationship between the impact parameter and the scattering angle (which can be read off from the above geometry) is
\[ b = R \cos\left(\frac{\theta}{2}\right) \; . \]
The derivative, which is very easy to compute, is
\[ \frac{db}{d\theta} = -\frac{R}{2} \sin\left(\frac{\theta}{2}\right) \; \]
and
\[ D(\theta,\phi) = \frac{R^2}{4} \; .\]
Integrating this expression over the entire solid angle gives
\[ \int d\Omega D(\theta,\phi) = \pi R^2 \; .\]
Certainly interesting and encouraging, but totally misleading, since the ‘potential’ for hard sphere scattering has compact support, a situation that most potentials of interest fail to possess.